GAMES101-6 20200228 20210708 Rasterization 2 anti - aliasing and Z - buffering

6 20200228/20210708 Rasterization 2 anti-aliasing and Z-buffering

Sampling Artifacts (Errors / Mistakes / Inaccuracies) in Computer Graphics

• 采样的例子

  • rasterization = sample 2d positions
  • photograph = sample image sensor plane

• video = sample time

• 采样瑕疵的例子 sampling artifacts

  • Jaggies (staircase pattern)

    

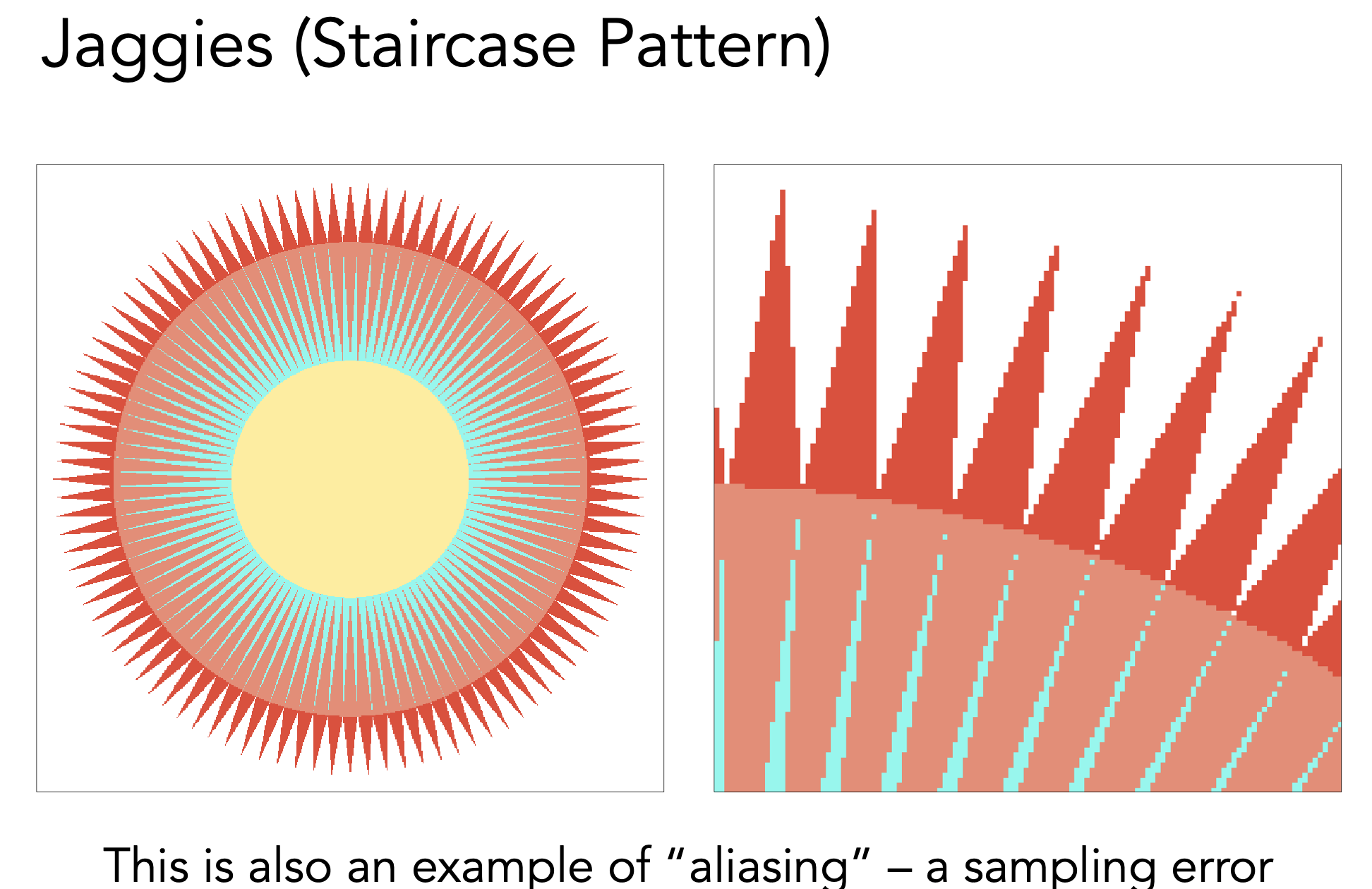
  • Moiré Patterns in Imaging

    

  • Wagon Wheel Illusion (False Motion)

    
    • 原因：人眼在时间上的采样跟不上运动速度

• 采样瑕疵的本质

  • Signals are changing too fast (high frequency), but sampled too slowly

Antialiasing Idea: Blurring (Pre-Filtering) Before Sampling

• 先模糊滤波再采样

  

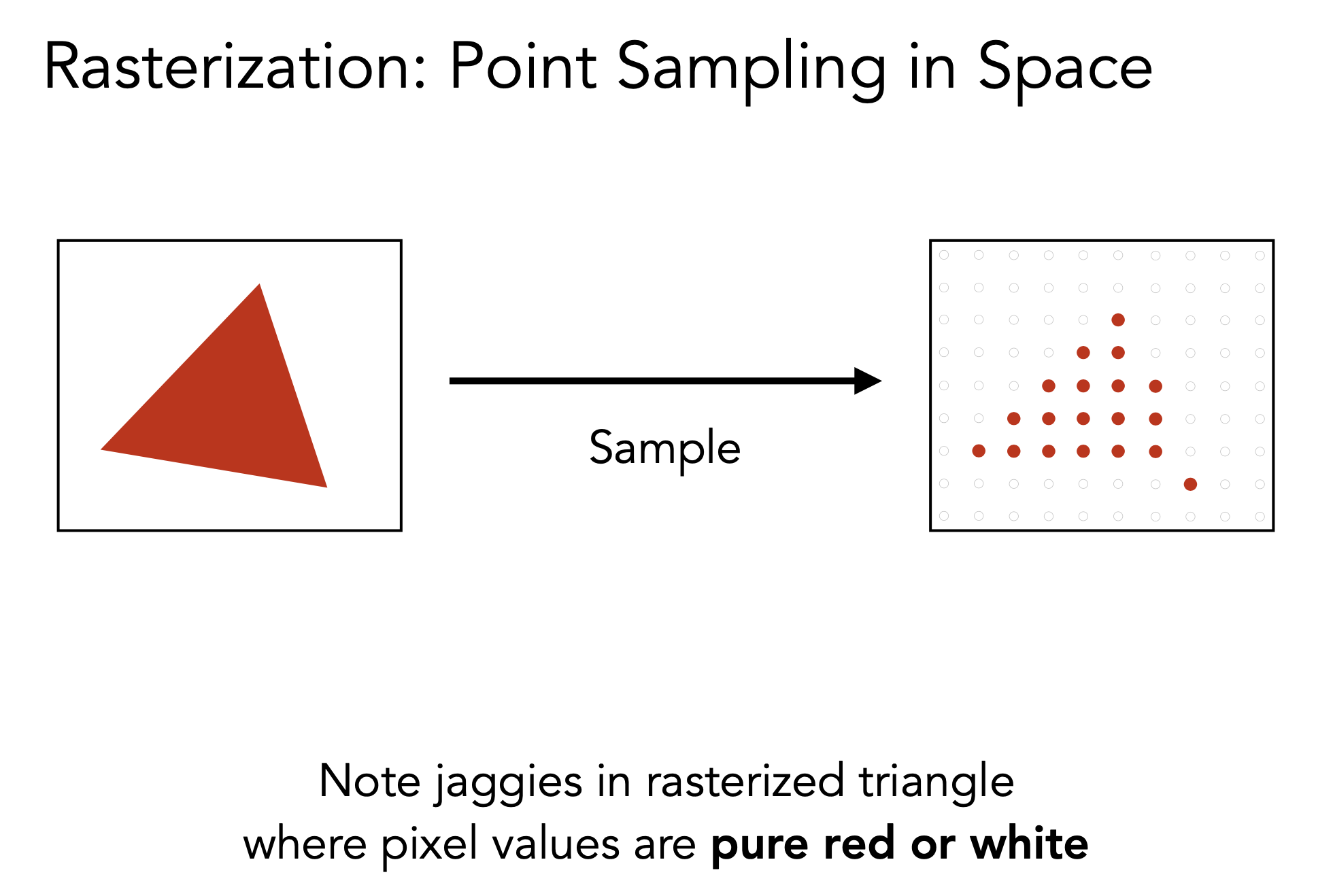
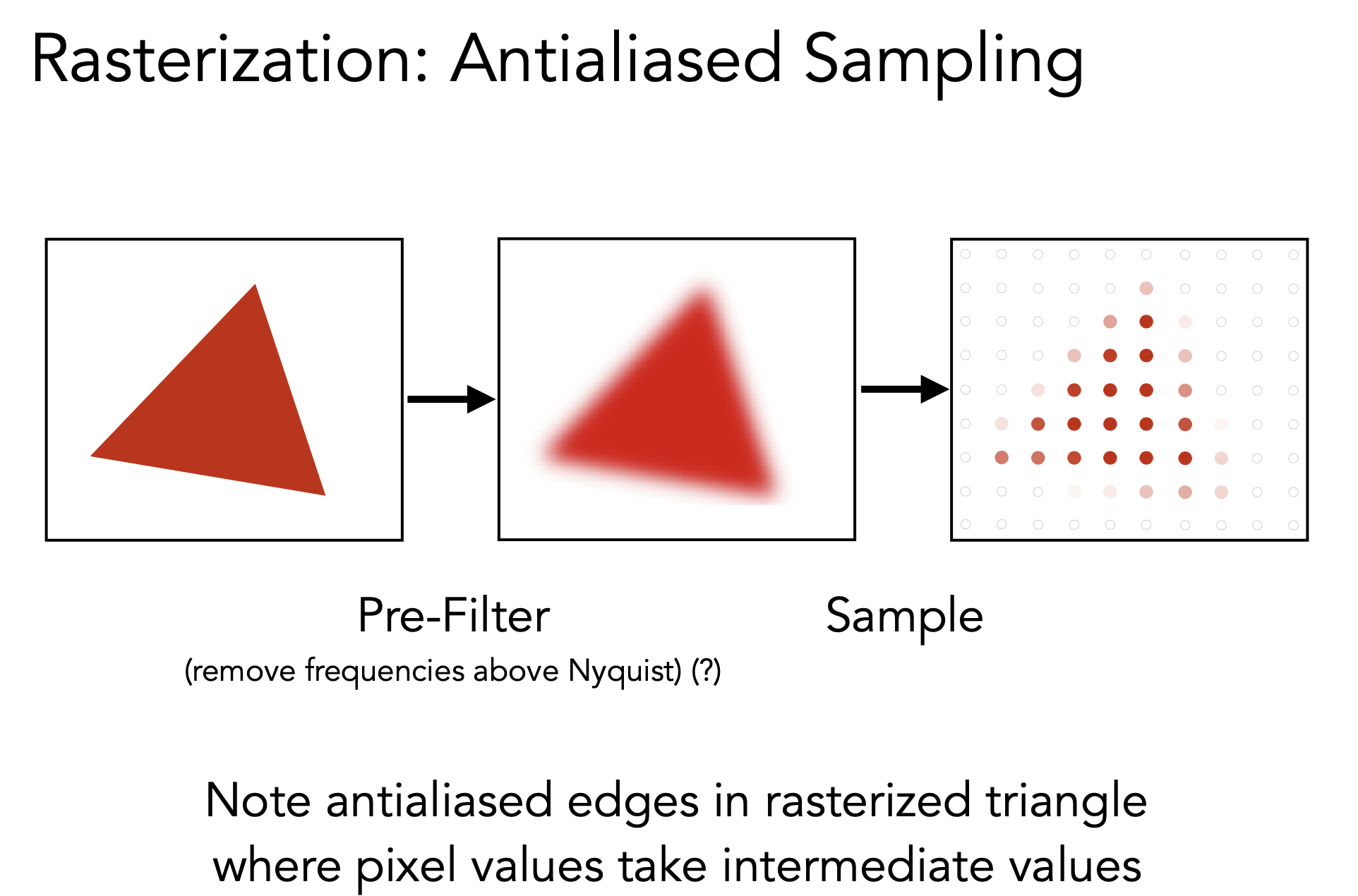
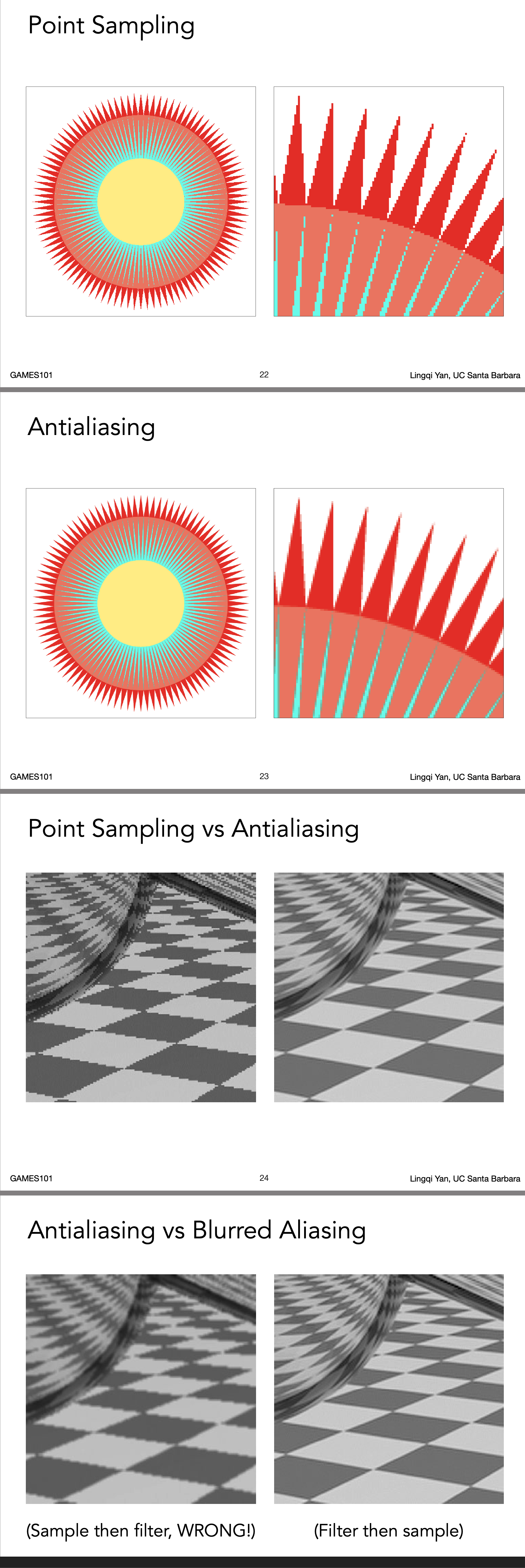
But why?

1. Why undersampling introduces aliasing?
2. Why pre-filtering then sampling can do antialiasing?

• Let’s dig into fundamental reasons

  And look at how to implement antialiased rasterization

• 为什么先采样再模糊不行

  • 先采样后 频谱已经发生了混叠
  • 此时再模糊 得到的结果还是混叠的频谱

Frequency domain 频域

• Frequencies

  

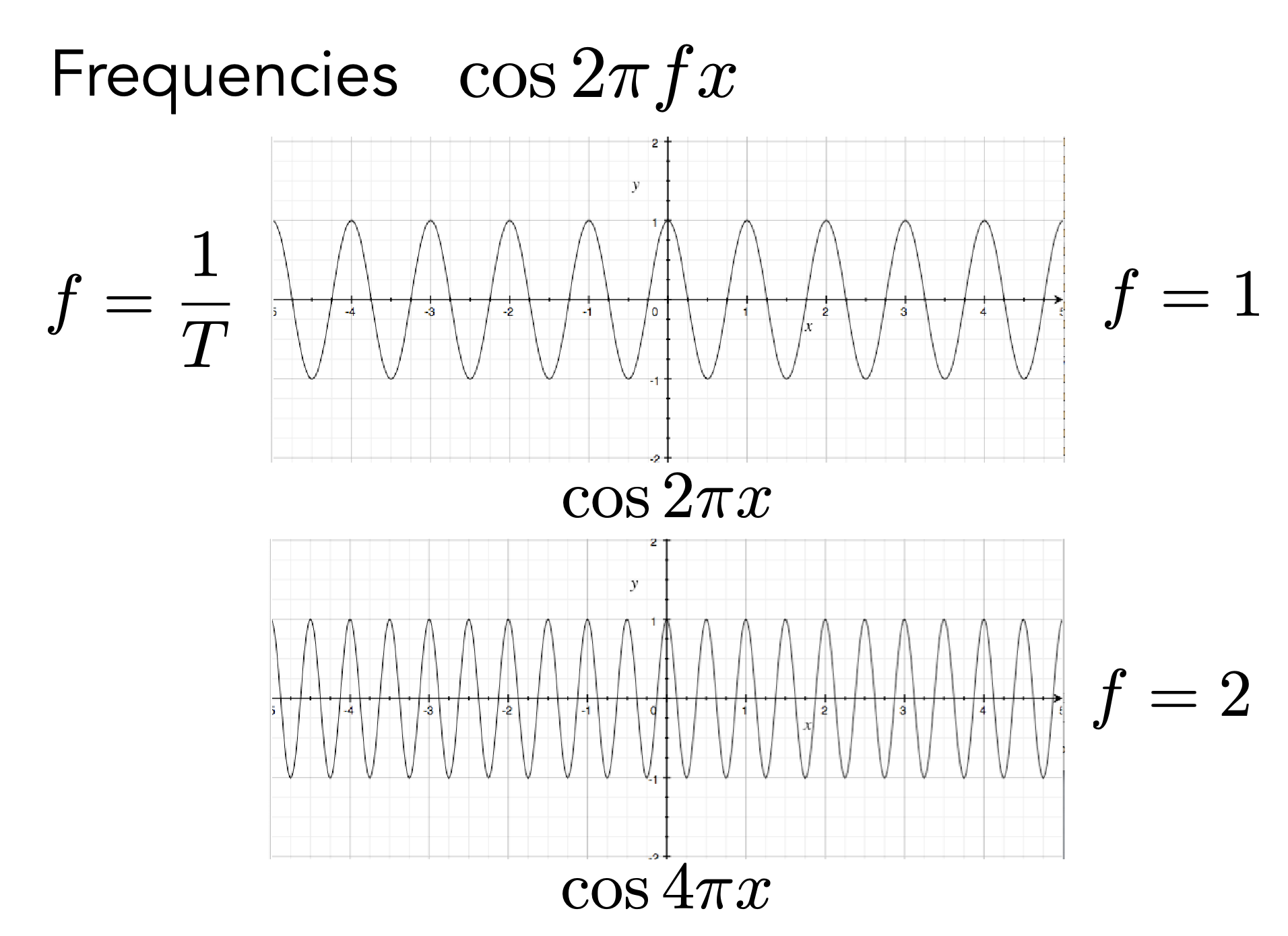
Fourier Transform

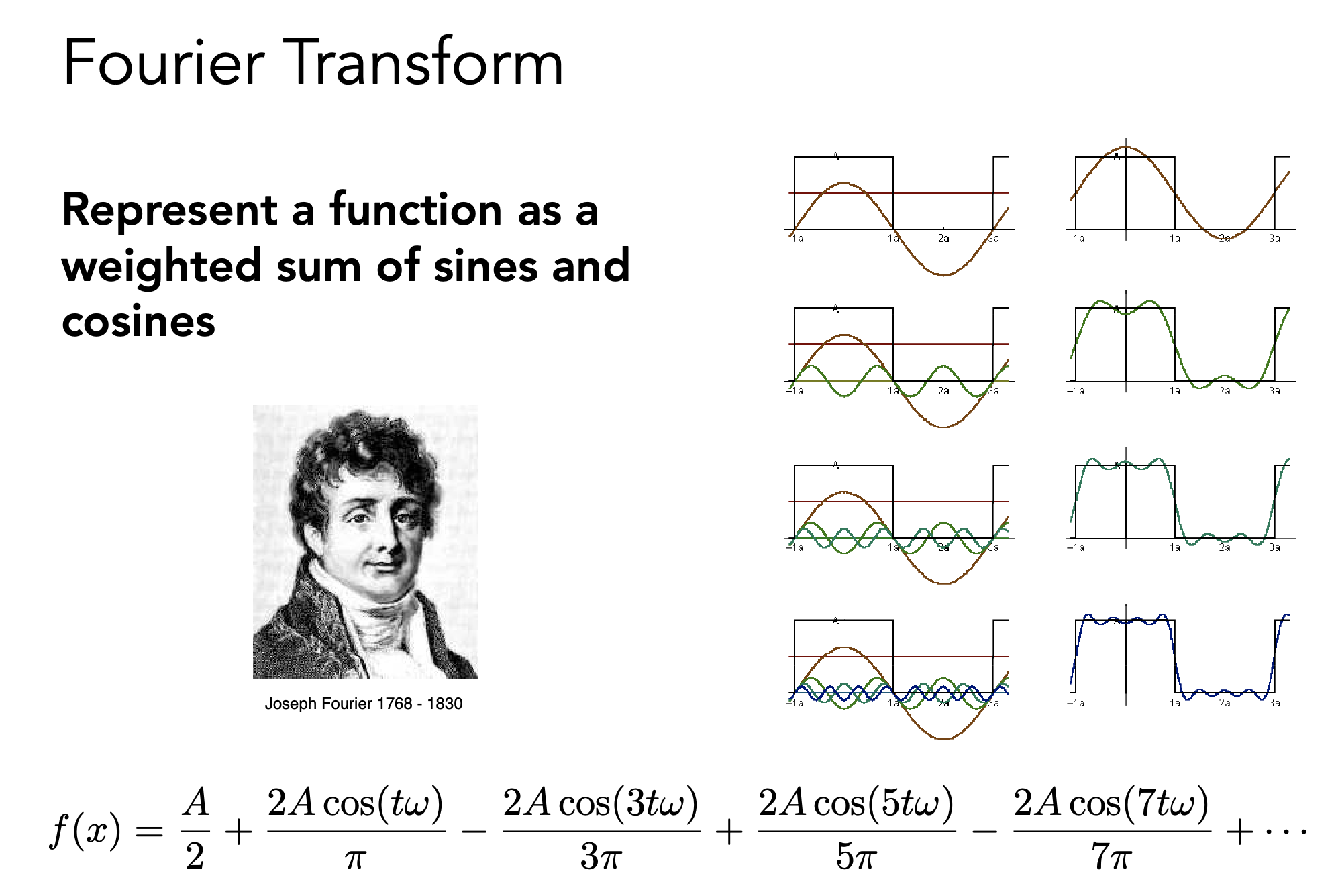
• 傅里叶级数展开：任何一个周期函数都可以写成一系列正弦余弦函数线性组合以及一个常数项

  • 任何一个函数都可分解为不同频率

• fourier Transform Decomposes A Signal into Frequencies 傅里叶变换（把一个函数变为另一个，或者反过来）把函数分解为不同频率的段并分别显示出来

  

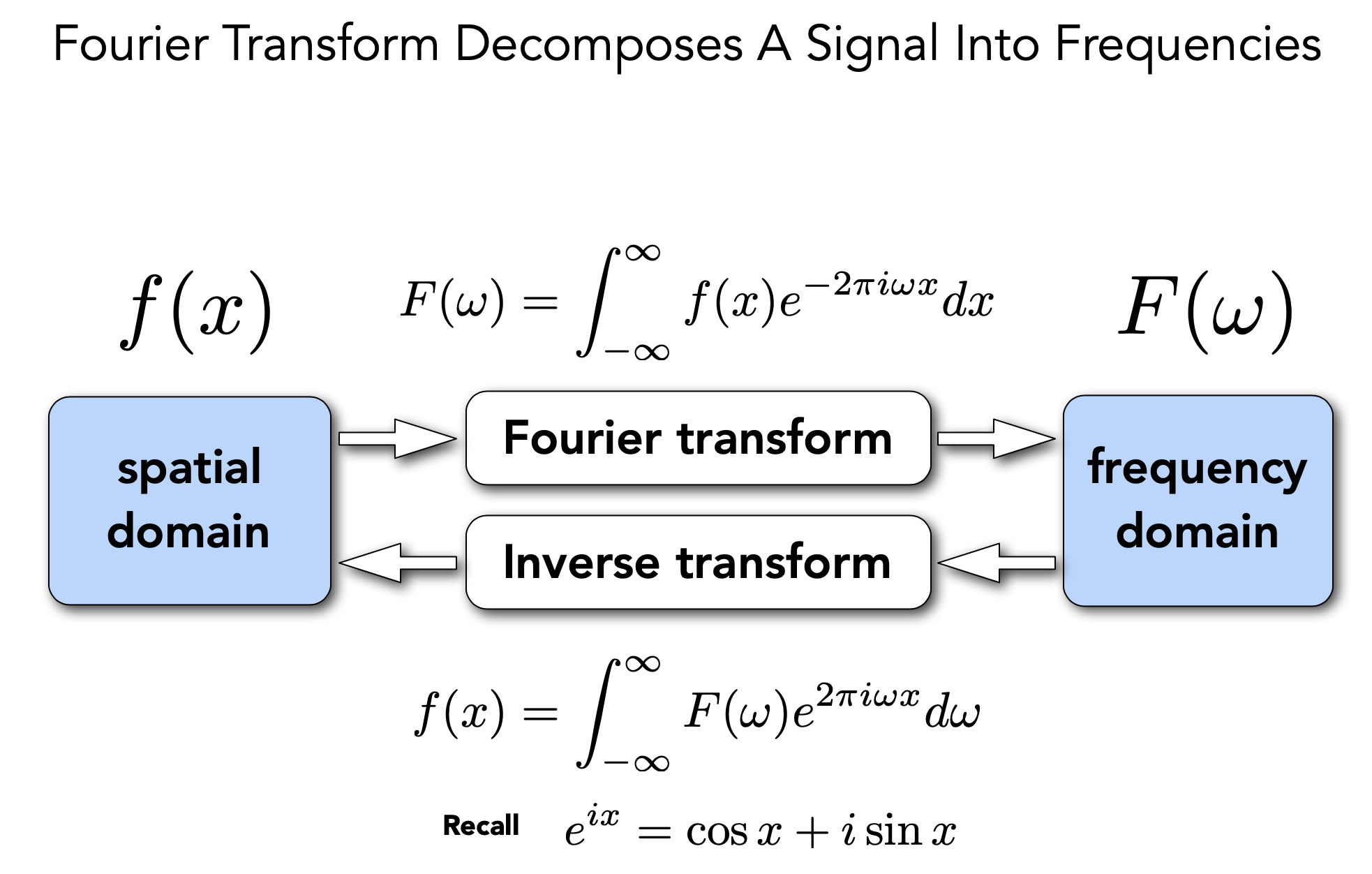
• Higher Frequencies Need Faster Sampling

  

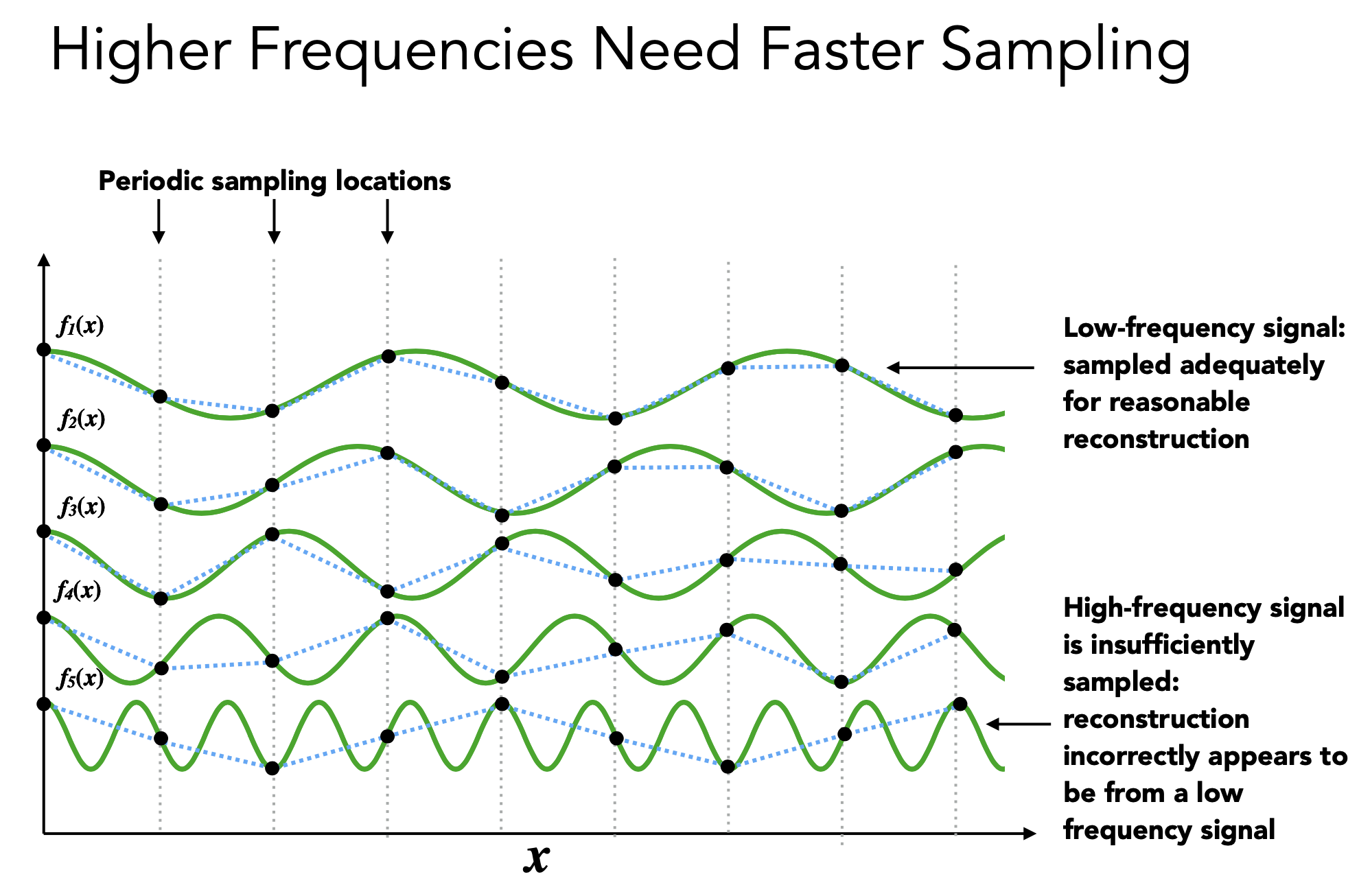
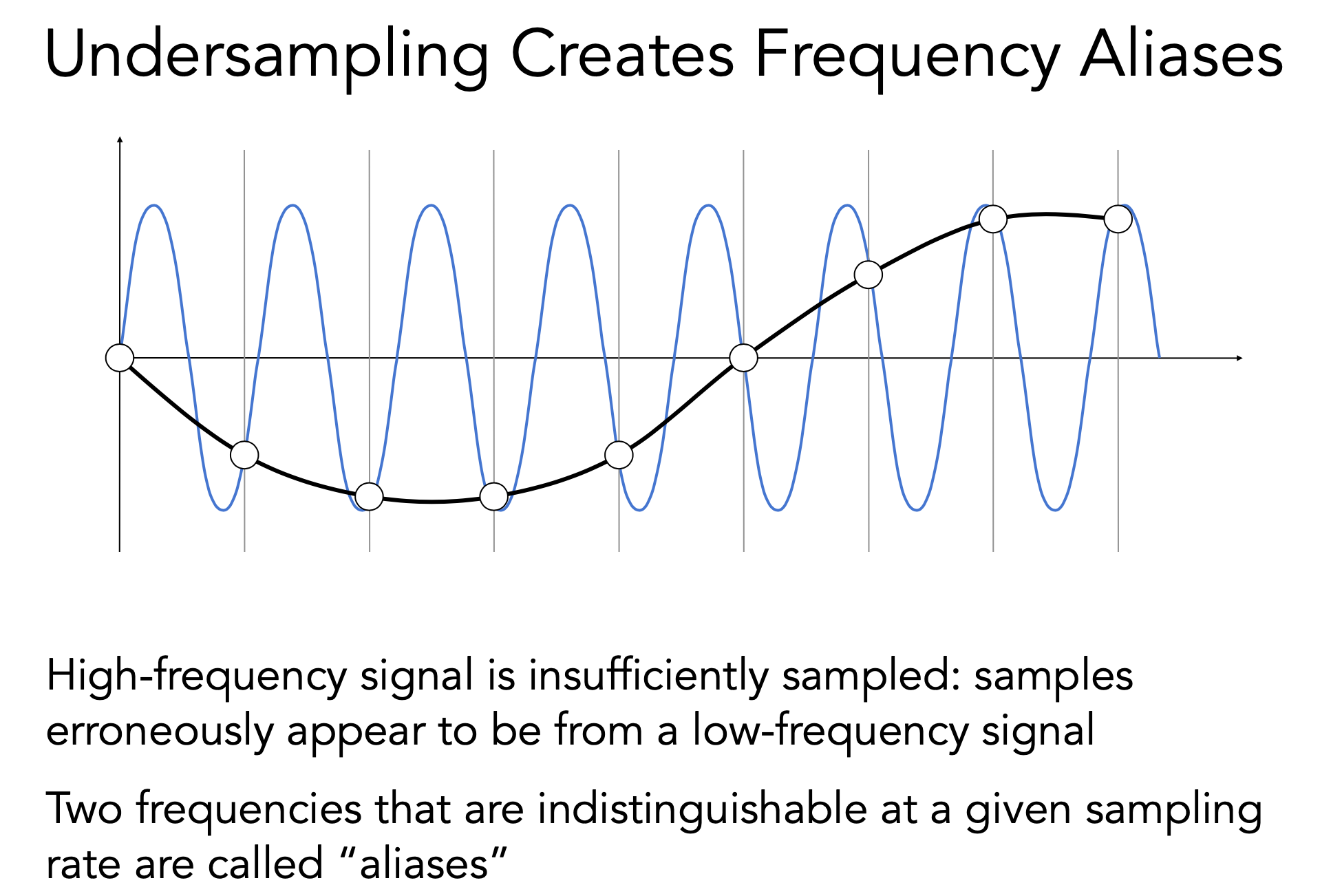
• Undersampling Creates Frequency Aliases 欠采样导致了频率瑕疵以频率定义走样：假如蓝色和黑色分别是两个不同的函数 二者采样方法相同 但本身频率不同 导致了采样结果相同

  

Filtering = Getting rid of certain frequency contents

• 傅里叶变换把图像从时域变成了频域

• 中心是最低频 周围是高频

• 多数信息集中在低频（中心）

• 水平和竖直亮线

  • 分析信号时会假设信号周期性重复（即假设图片水平重叠放置 AAAA）
  • 但实际上并不重复
  • 那么在左右边界部分会产生剧烈信号变化 - 产生高频
  • 则产生白线
  • 若分析单幅内容 可忽略

• 高通滤波（抹掉低频信号）可得到图像内容轮廓边界 - 和周围内容相差巨大 - 信号变化非常大 - 高频信号

  

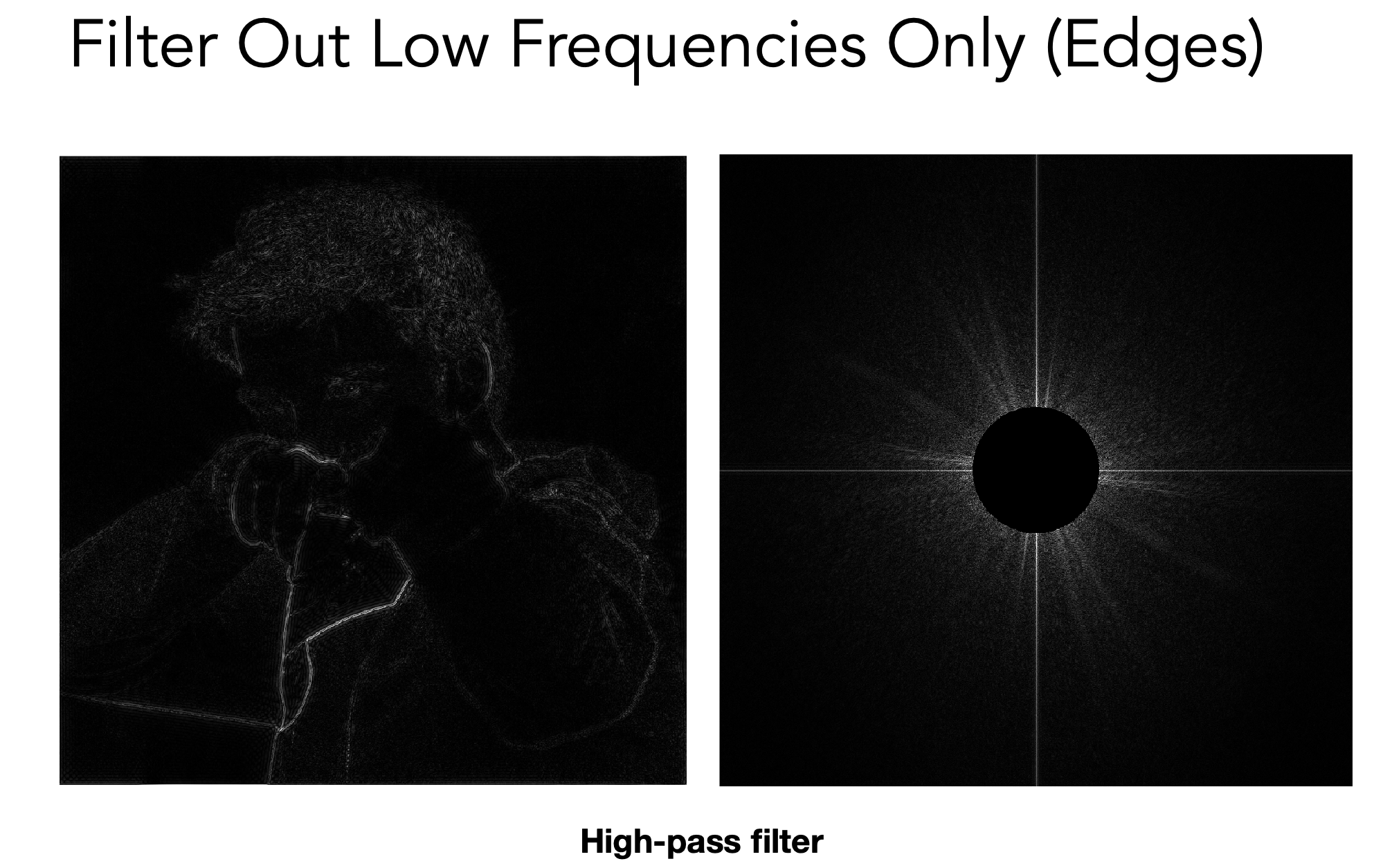
• 低通滤波（只有低频信号通过，抹掉高频信息）

  
  • 边界被抹去
  • 水波纹

• 去掉了高和低频率信息

  
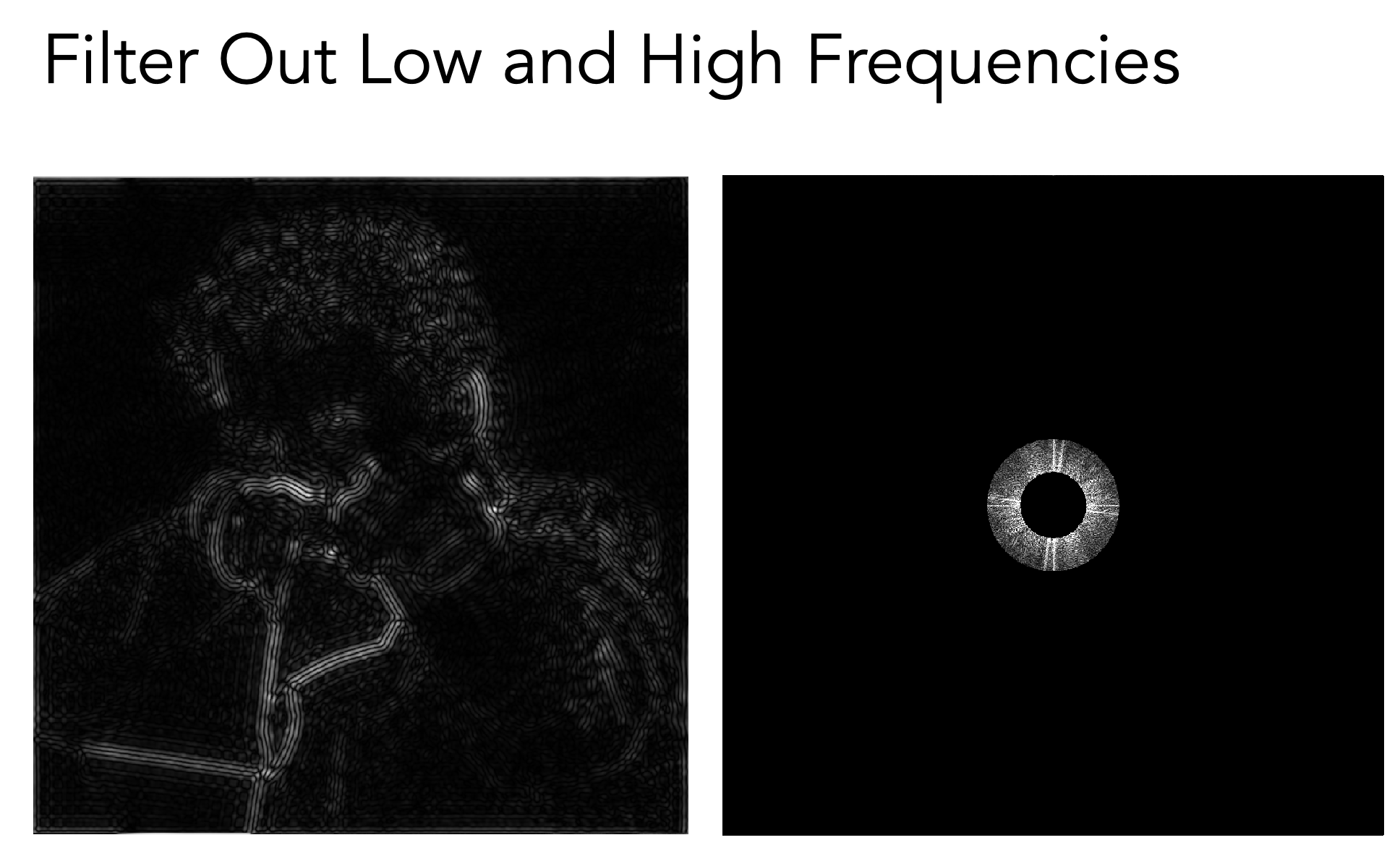
  • 提取到了不太明显的轮廓特征
  • 数字图像处理

Filtering = Convolution 卷积 (= Averaging) 加权平均

• Convolution 卷积

  

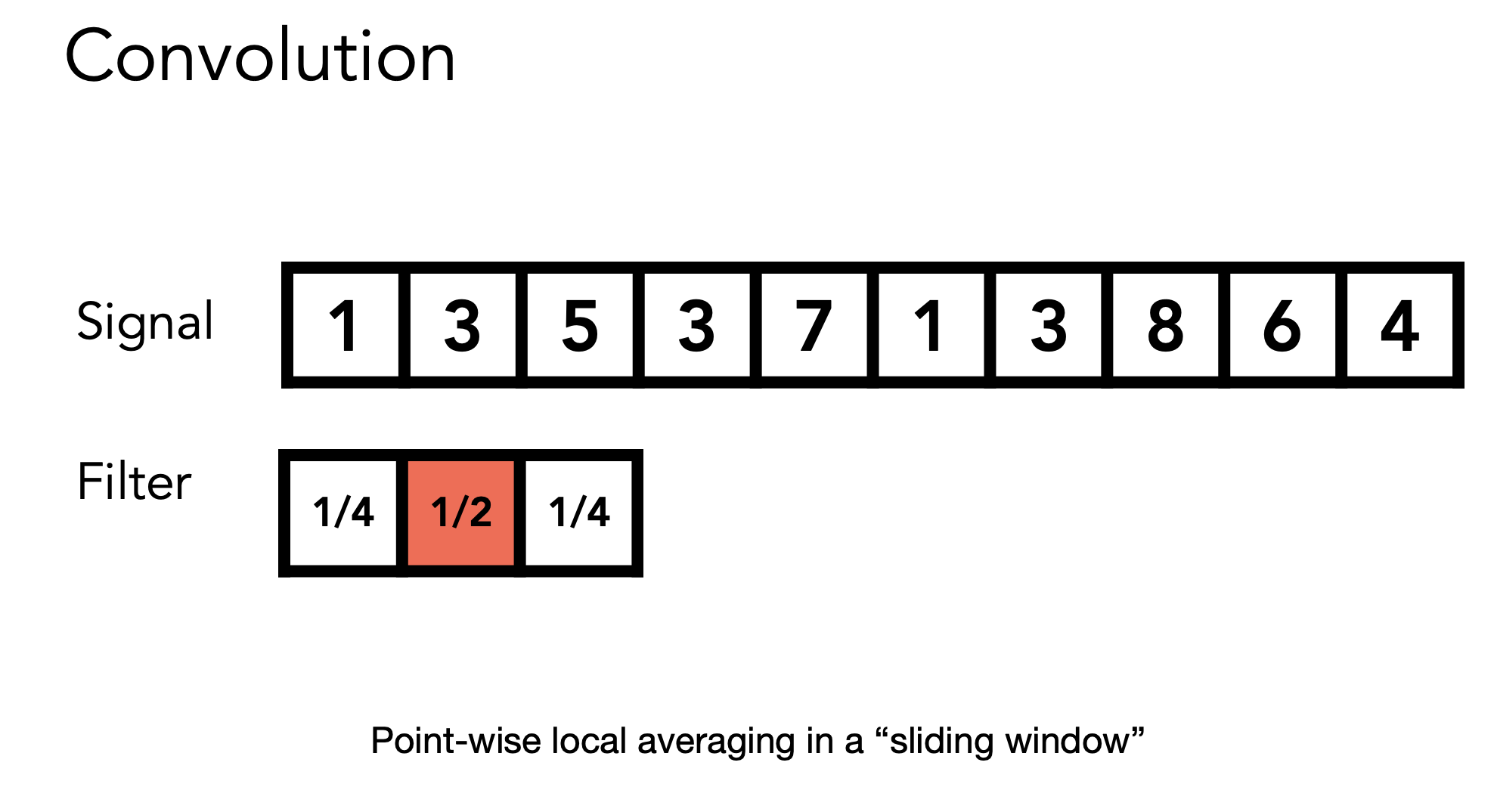
• 图形学中的简化定义

  • 卷积：通过窗口来进行点乘获取中心值（相当于加权平均）

• Convolution Theorem（卷积定理）

  
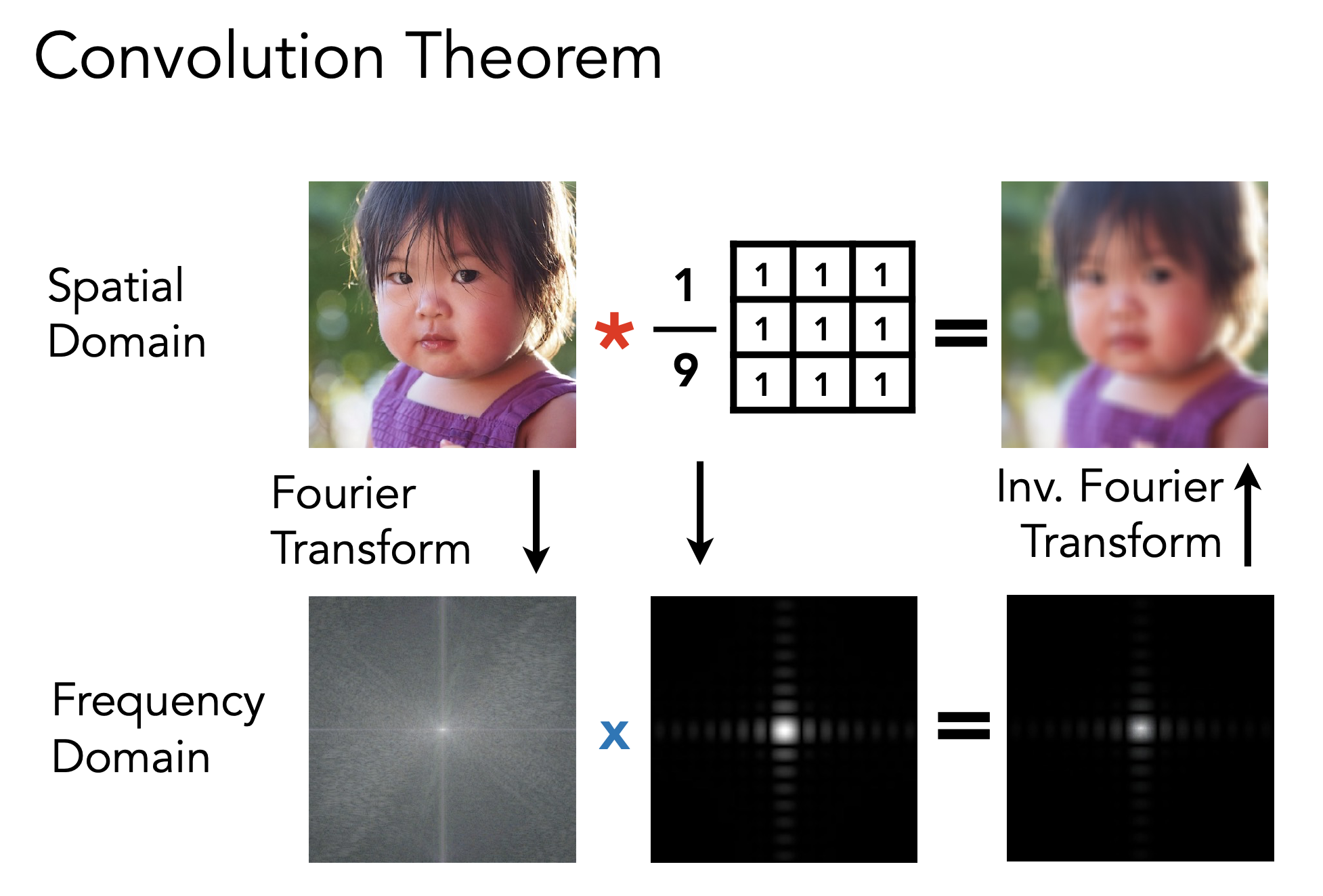
  • Convolution in the spatial domain is equal to multiplication in the frequency domain, and vice versa - 在时域上想对信号进行卷积相当于在频域上进行乘积，反之亦然
  • Option 1:
    • Filter by convolution in the spatial domain
  • Option 2:
    • Transform to frequency domain (Fourier transform)
    • Multiply by Fourier transform of convolution kernel
    • Transform back to spatial domain (inverse Fourier)

Box Filter 低通滤波器

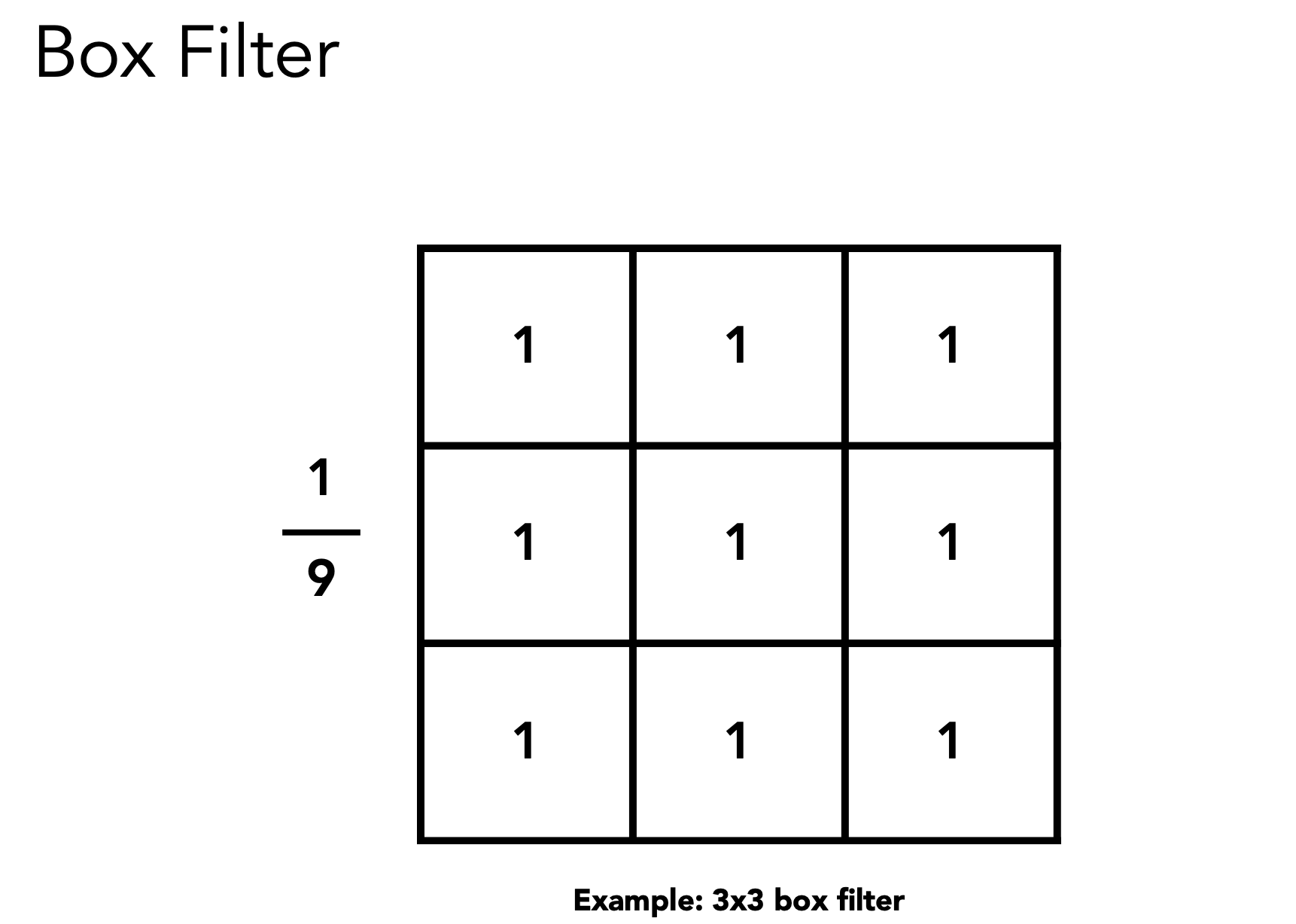
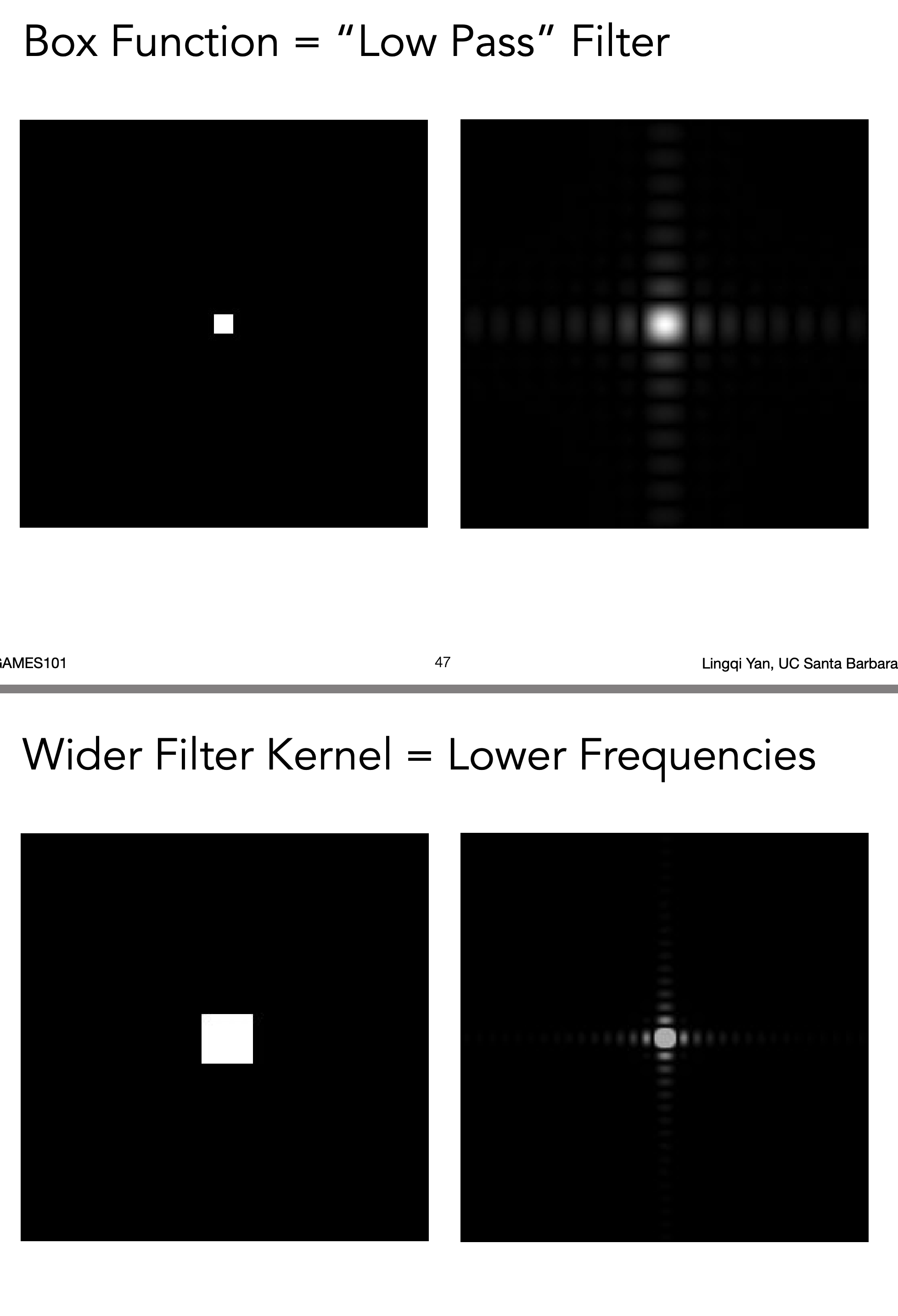
• box 越大结果越模糊（留下的频率越低）
  • 相当于画笔变大
• 考虑极端情况
  • box 超级大 - 只有最中间有采样信息
  • box 超级小 - 全部频率都被留下来

Sampling = Repeating Frequency Contents

• 冲激函数（某些位置有值有些没有，为0）

  
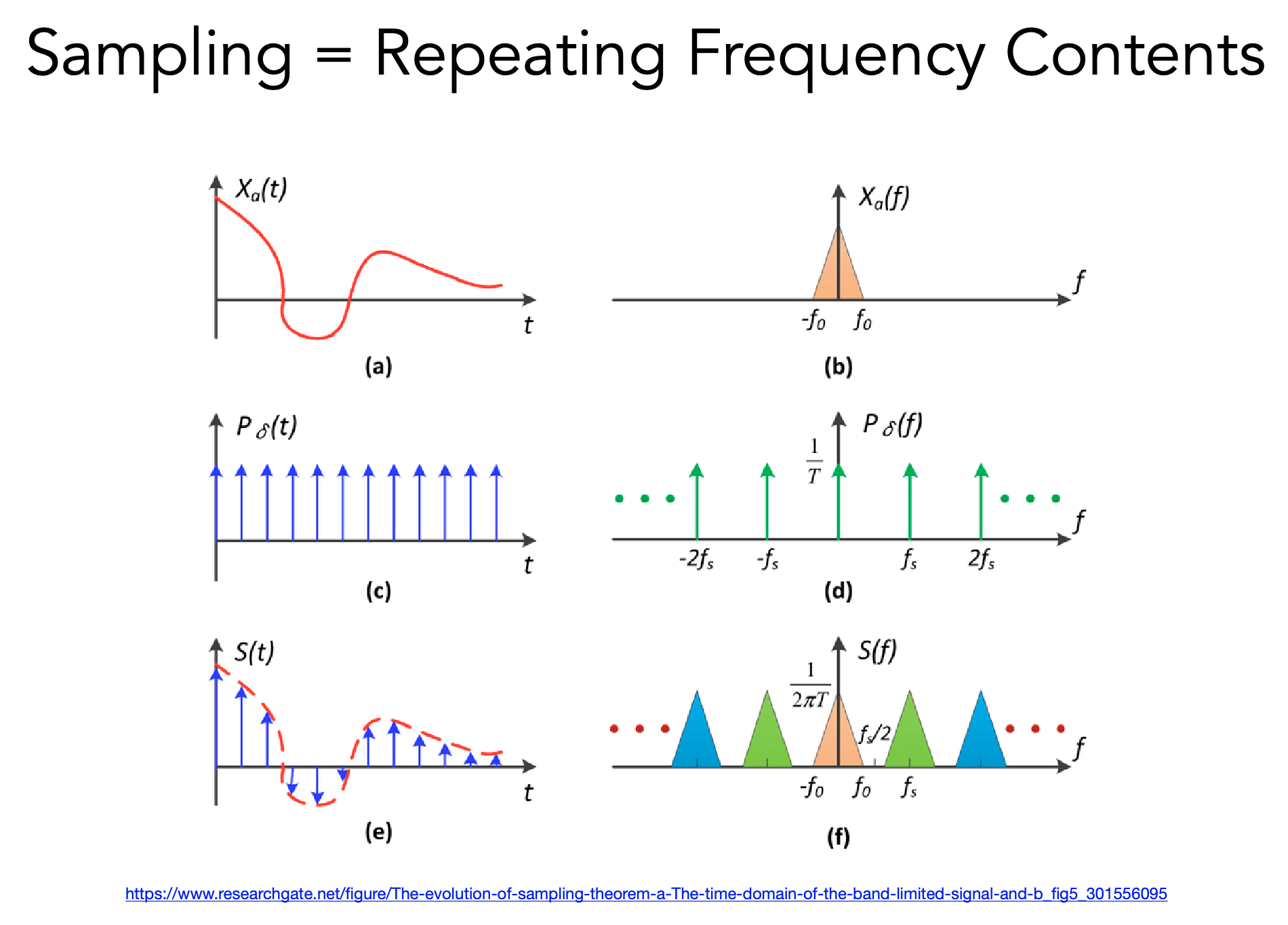
  • 采样：给定函数与冲激函数相乘得到采样结果
  • 采样（从频域角度理解）：就是在重复原始信号的频谱

$$时域的乘积 = 频域的卷积$$

• 为什么会走样

  
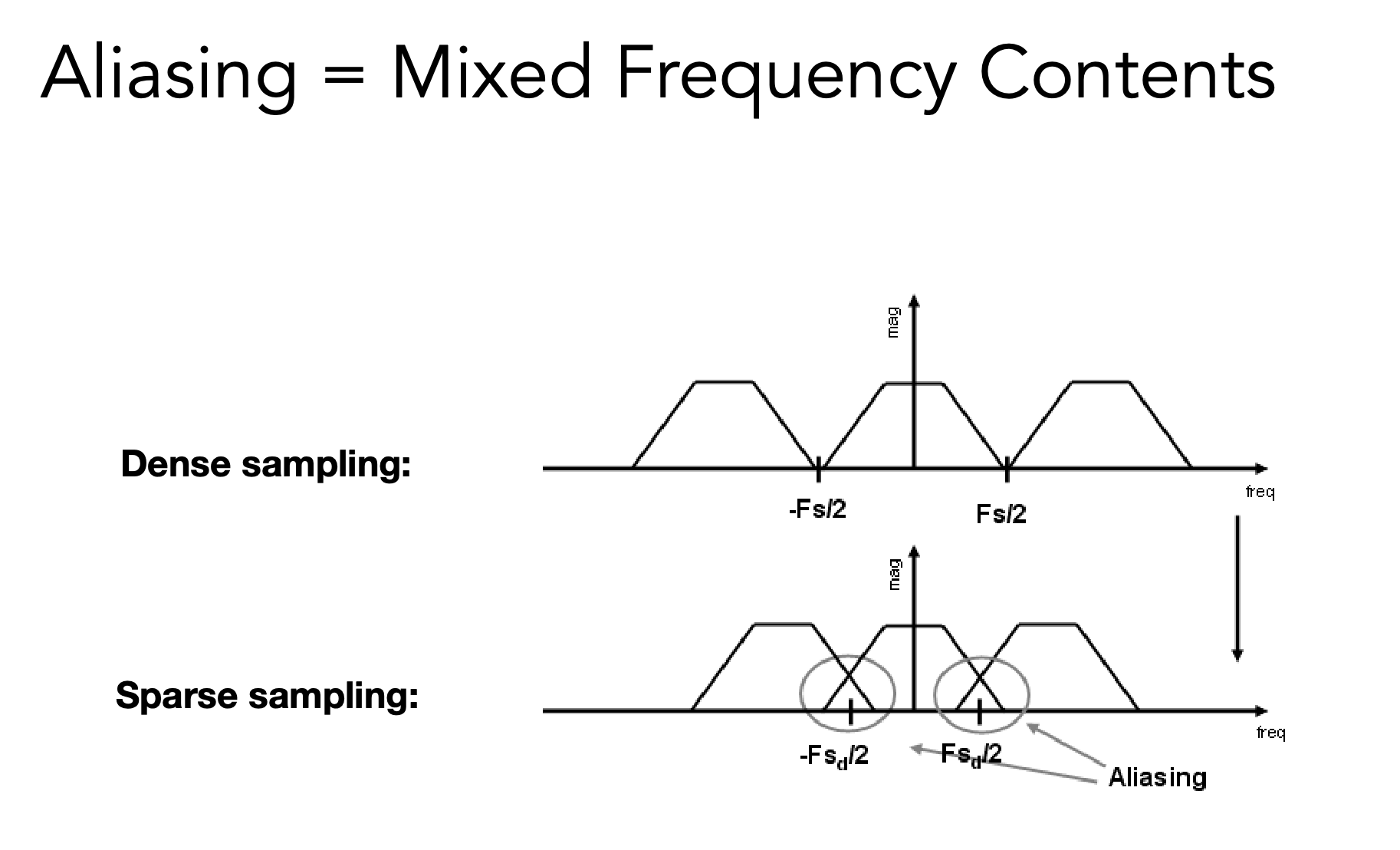
  • 采样率不足（不够快），导致原始信号复制粘贴距离不够大，频率的频谱发生了混叠，即走样
  • 相当于采样低 = 稀疏采样

Anti-Aliasing

• How Can We Reduce Aliasing Error?
• Option 1: Increase sampling rate
  • Essentially increasing the distance between replicas in the
    Fourier domain
  • Higher resolution displays, sensors, framebuffers…
  • But: costly & may need very high resolution
• Option 2: Antialiasing
  • Making Fourier contents “narrower” before repeating
  • i.e. Filtering out high frequencies before sampling
• 步骤
  • 先卷积
  • 再采样

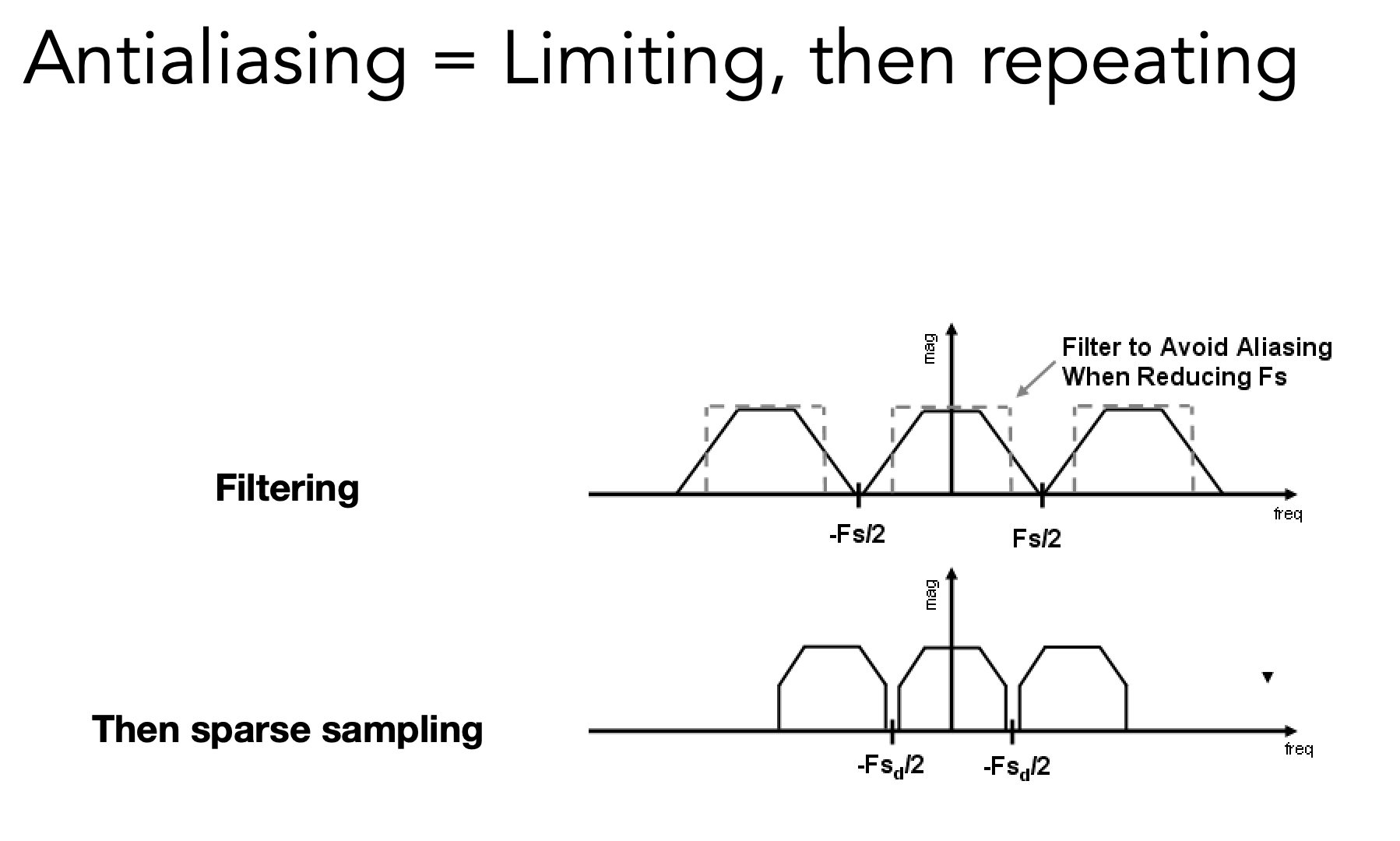
• 模糊之后的频谱覆盖范围小

• 所以采样堆叠几率小

• 如何模糊

  • 用一定大小的低通滤波器来处理图像

    

Antialiasing by averaging values in pixel area

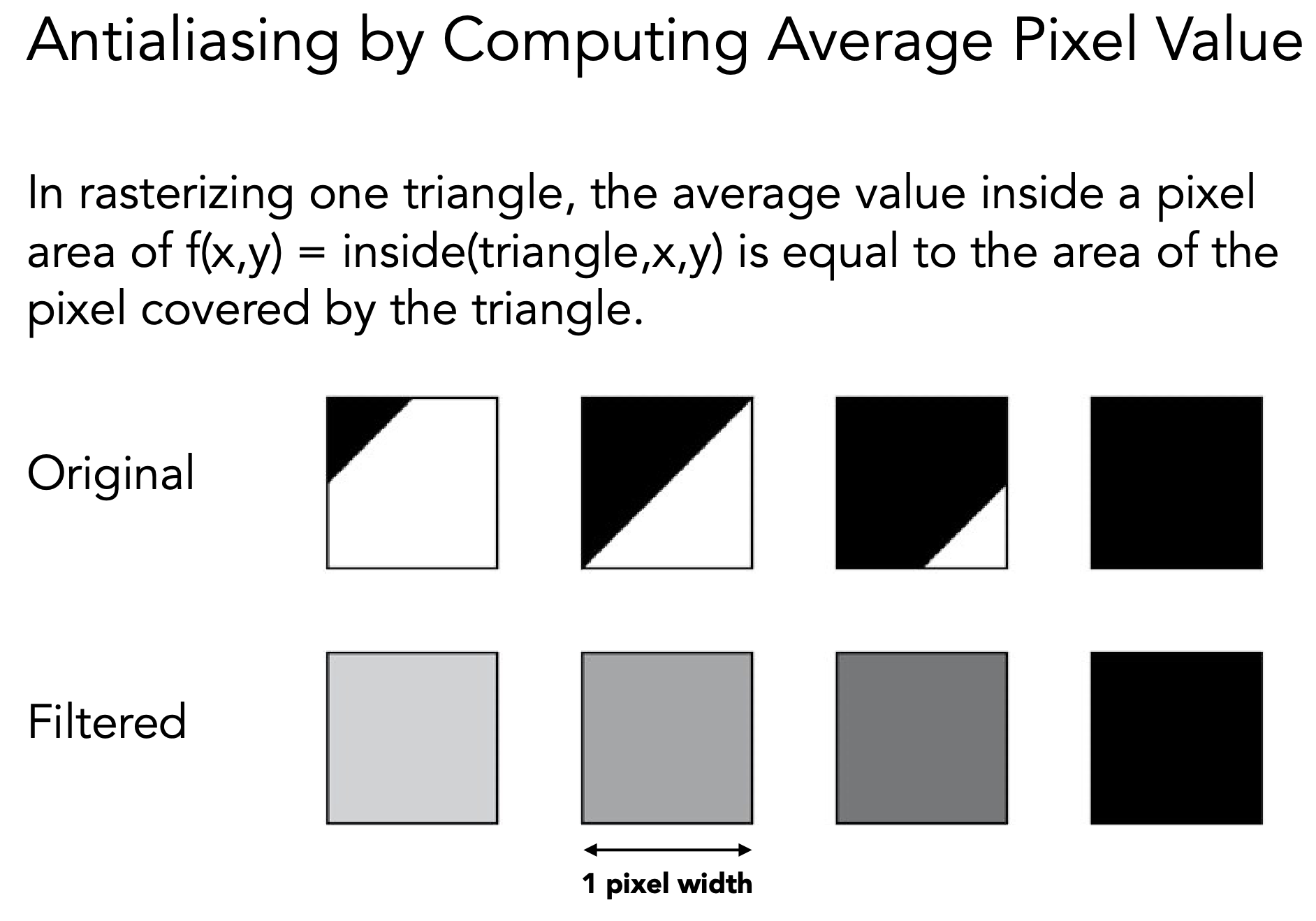
• Solution:

  • Convolve f(x,y) by a 1-pixel box-blur
    • convolving = filtering = averaging
  • Then sample at every pixel’s center

• 怎么把三角形在像素内覆盖的区域算出来：

Antialiasing By Supersampling (MSAA)

解决的是对信号的模糊操作 不是靠提升分辨率解决问题 只是为了解决三角形覆盖问题

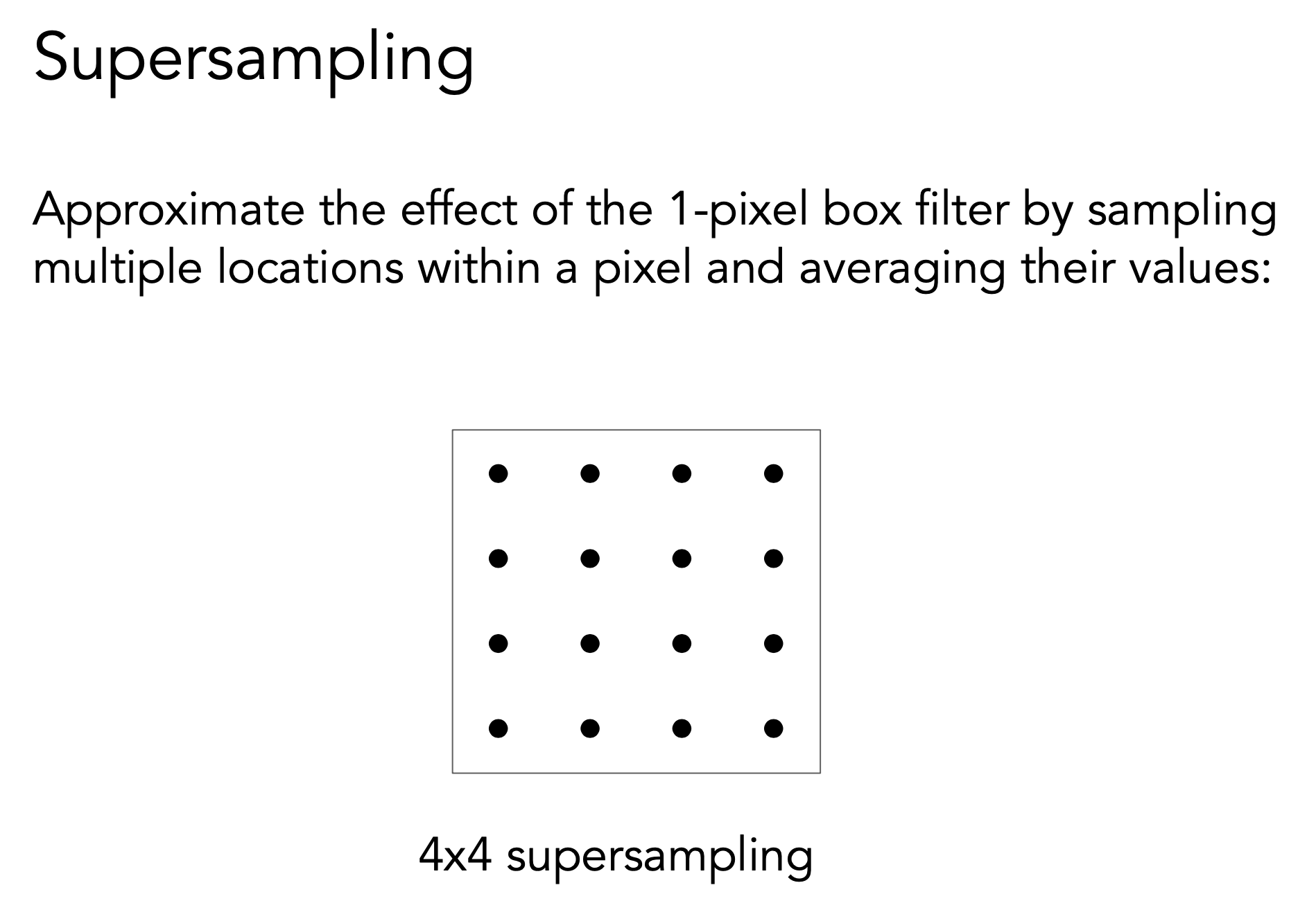
• 给像素内部加采样点 看像素覆盖率

Antialiasing Today

• No free lunch!What’s the cost of MSAA?
  • 增加了计算量
• Milestones (personal idea)
  • FXAA (Fast Approximate AA)
    • 和采样无关 相当于后期处理
    • 得到一幅图 有锯齿 找到边界 将有锯齿的边界换成没有锯齿的边界
  • TAA (Temporal AA)
    • 复用上一帧信息 在当前帧不引入新信息
• Super resolution / super sampling 超分辨率
  • From low resolution to high resolution
  • Essentially still “not enough samples“ problem
  • DLSS (Deep Learning Super Sampling)
    • 一切猜测 深度学习都适合