4 20200221 / 20210705 Transformation Cont.
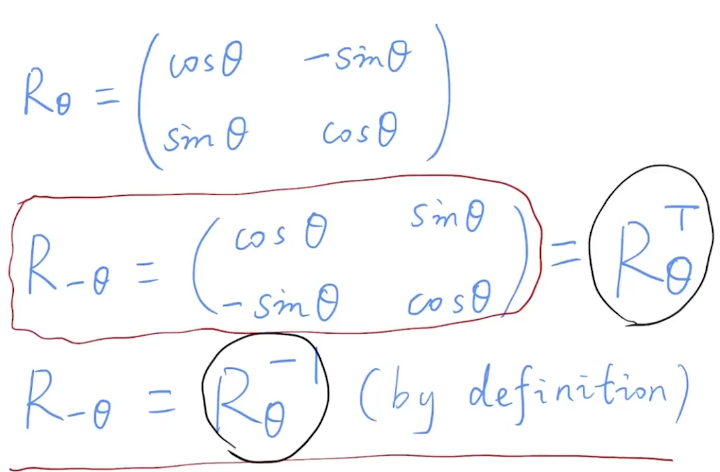
旋转的逆就是旋转的转置(正交)
3D transformations
Viewing (观测) transformation
- View (视图) / Camera transformation
- Projection (投影) transformation
- Orthographic (正交) projection
- Perspectve (透视) projection
3D transformations
Use homogeneous coordinates again:
- 3D point = (x, y, z, 1]
- 3D vector = (x, y, z, 0)
In general, (x, y, z, w) (w != 0) is the 3D point:
(x/w, y/w, z/w)
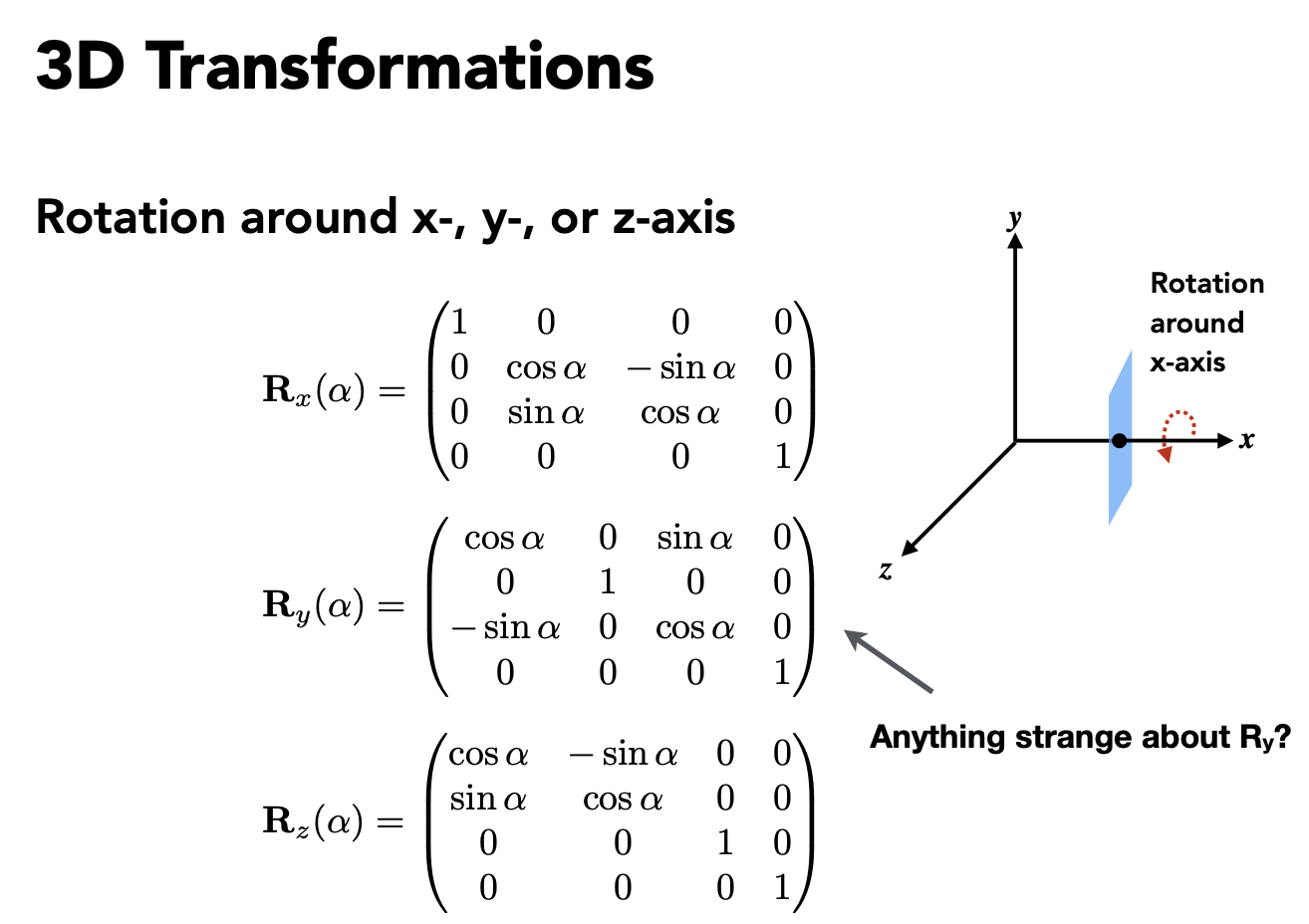
Rotation
- 循环对称使得y的矩阵和xz不同,因为是 z 叉乘 x 而不是 x 叉乘 z,所以符号反
3D Rotations
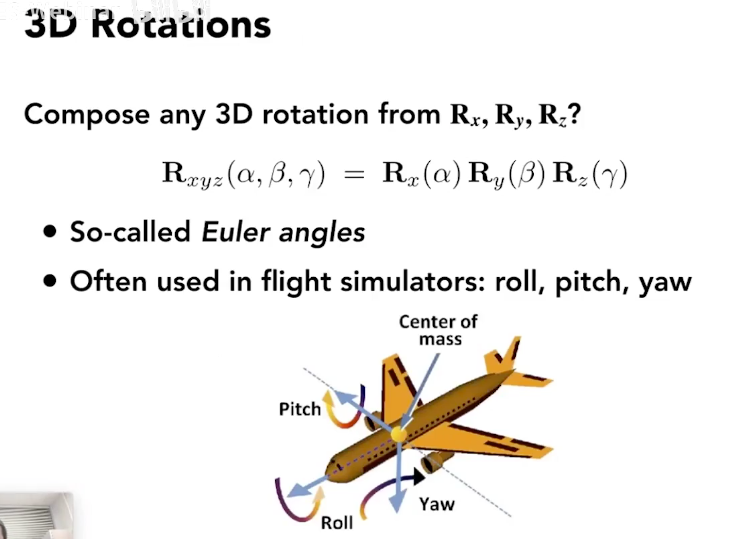
把任意旋转拆解为 x/y/z 旋转
Rodrigues’ Rotation Formula

- 默认轴过原点,方向为 $n$
- 若要沿着任意轴旋转
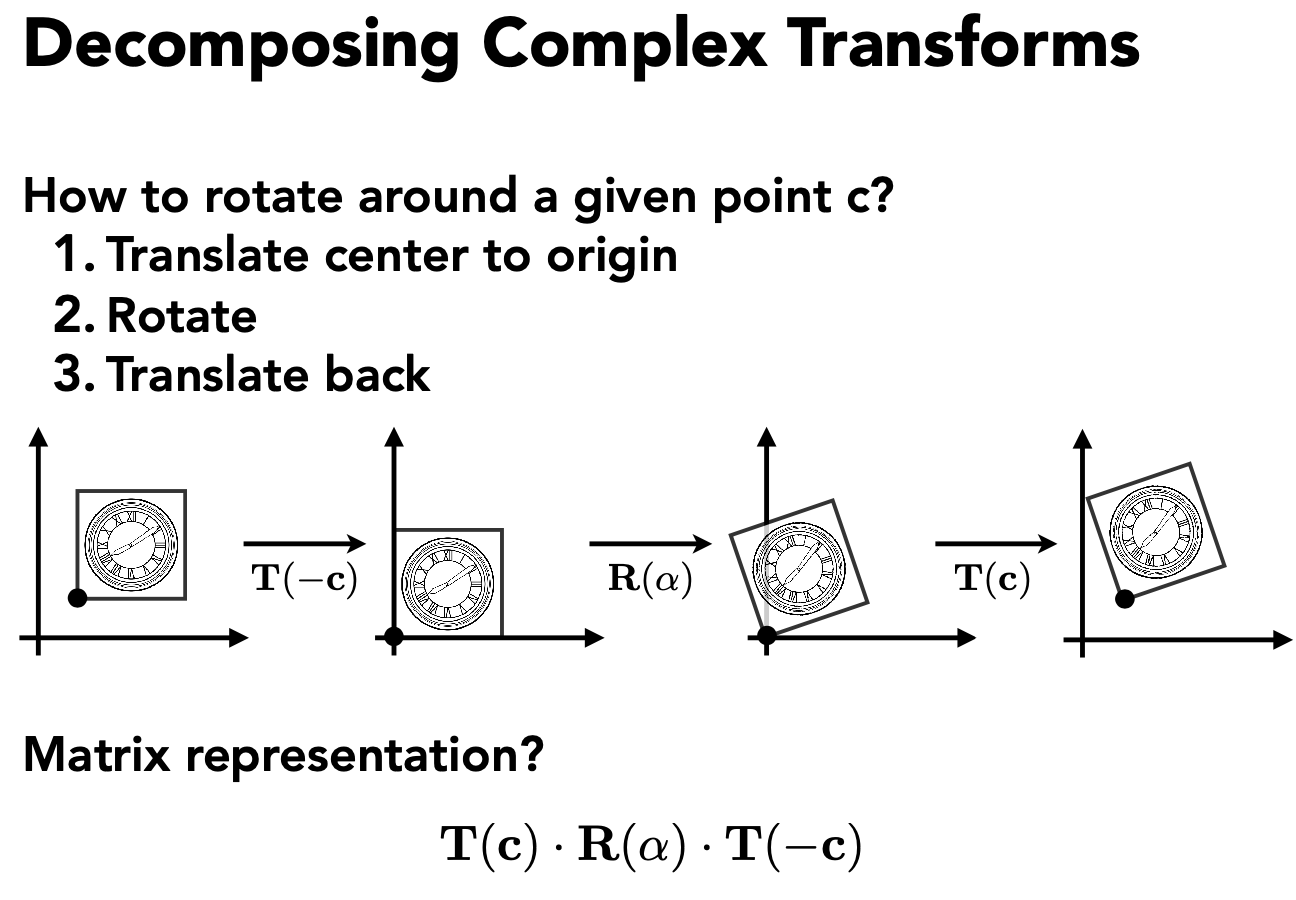
- 先把旋转的起点平移到原点
- 旋转后再平移回来(逆操作)
- 四元数 ()的引入是为了旋转的差值应用
- 转 10°和转 30°的均值并不是转 20°
Viewing transformation
View/ Camera transformation (视图/相机变换)
what is view transformation (MVP)
- Think about how to take a photo (MVP)
- Find a good place and arrange people (model transformation) 找物体位置 - 模型变换
- Find a good “angle” to put the camera (view transformation) 找相机位置 - 视图变换
- Cheese! (projection transformation) - 投影变换
- Think about how to take a photo (MVP)
How to perform view transformation
- Define the camera first
- Position $\vec e$
- Look-at / gaze direction
- Up direction $\hat t$
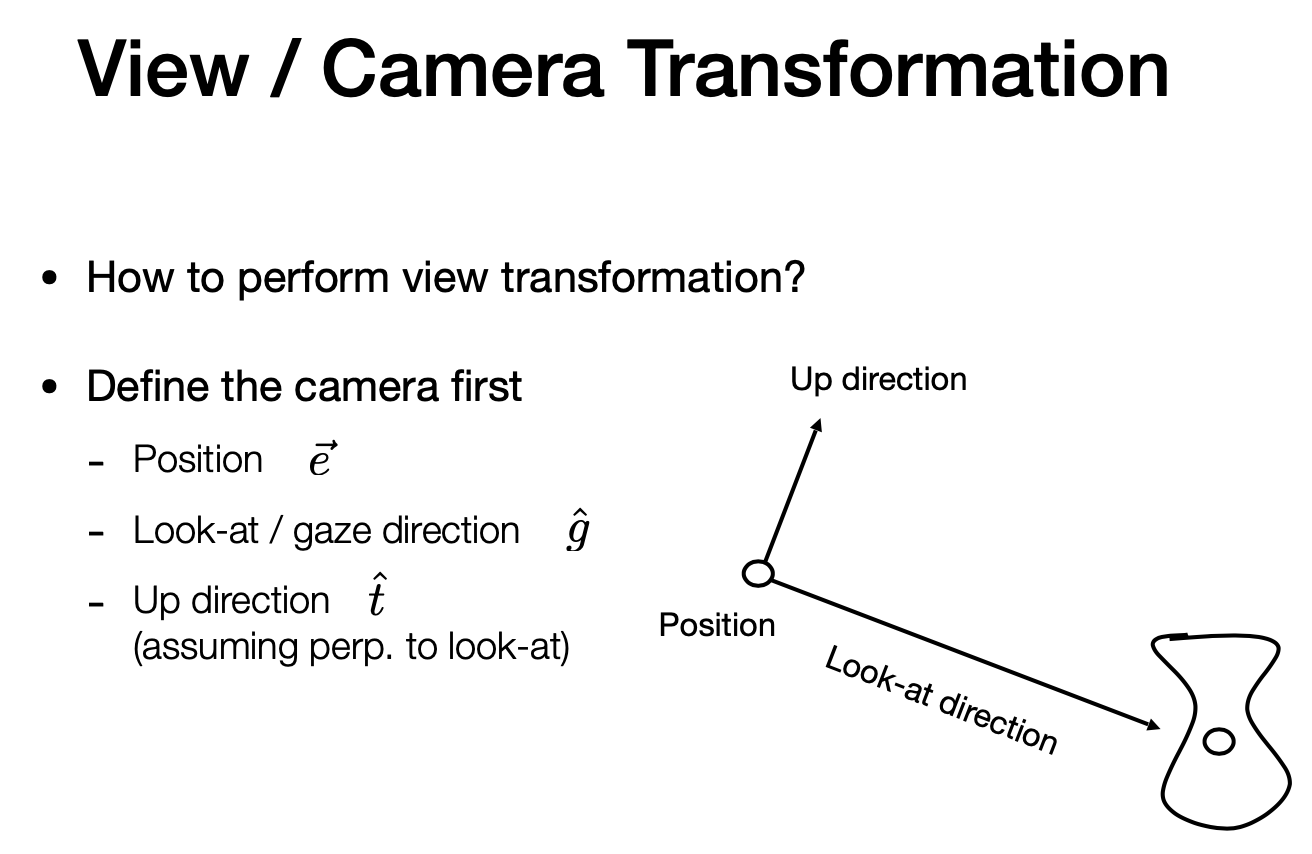
- Define the camera first
Key observation
如果相机和所有物体一起移动,那么成像一致
所以把相机位置固定到原点沿着-z方向看(所有物体的位置也做变换)
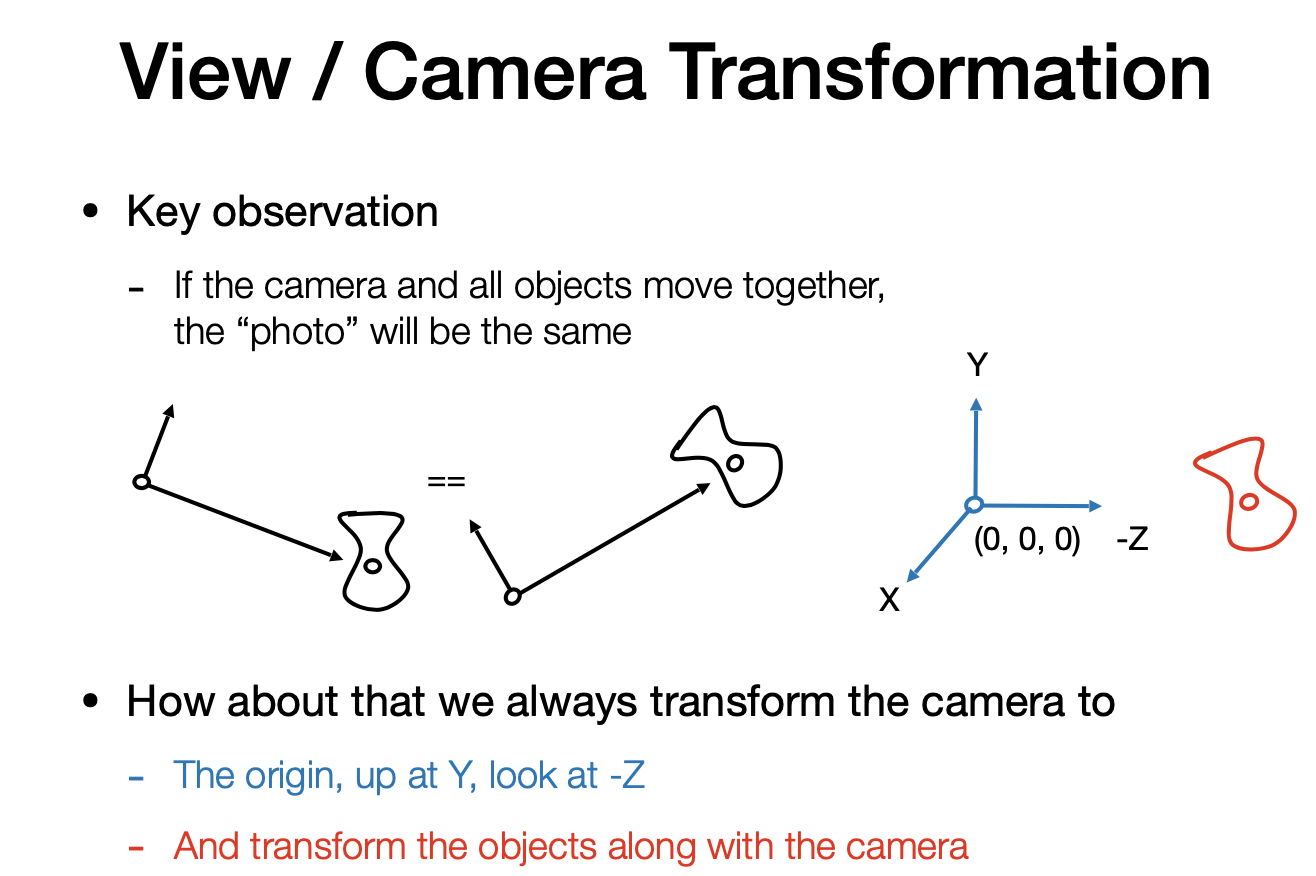
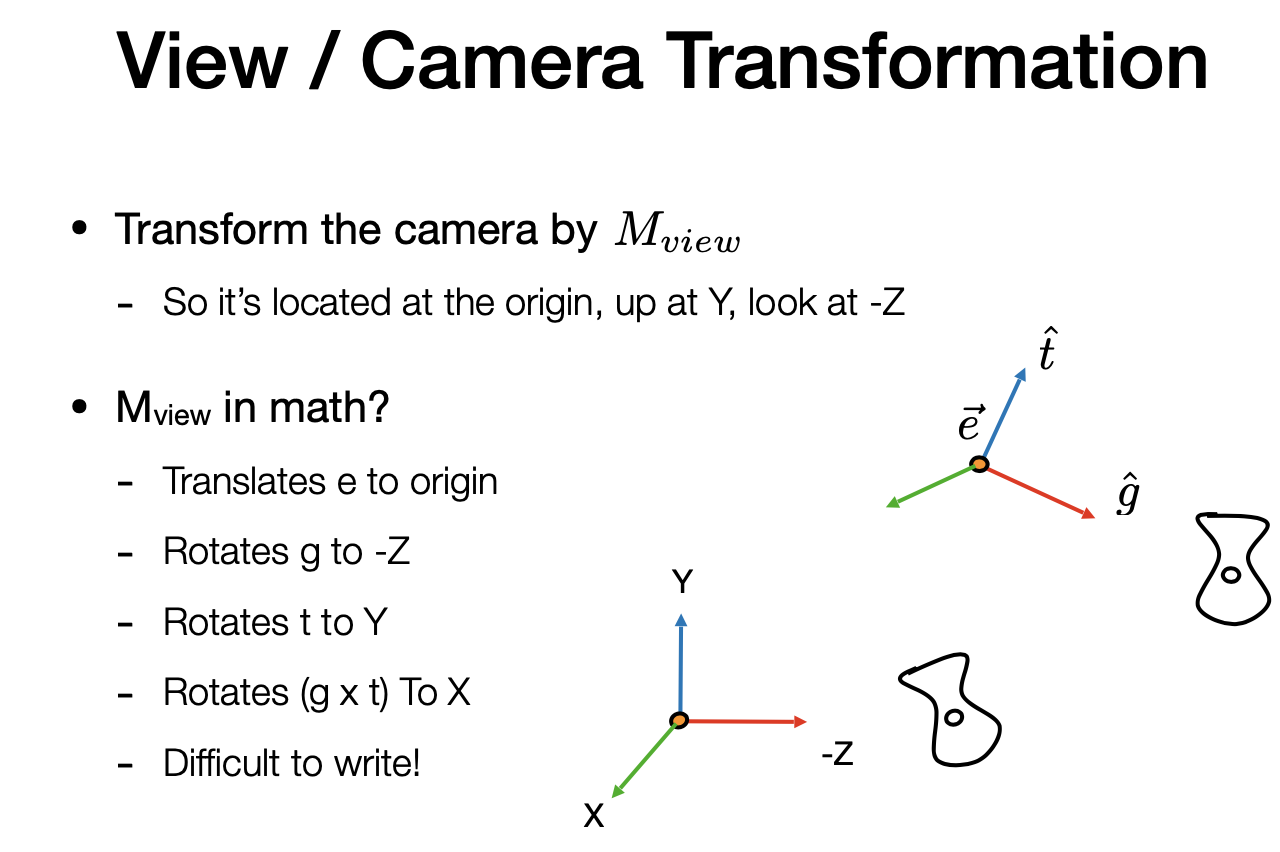

先平移再旋转
- 先把中心移动到原点(平移)
- 将所看方向旋转至 -z 方向
- 将 up 方向旋转到 y 方向
- $g \times t$ 旋转到 x 方向
正着写难写
$g \rightarrow -Z, t \rightarrow Y, (g · t \rightarrow X)$
反过来写好写
$X \rightarrow (g · t), Y \rightarrow t, Z \rightarrow -g$
(先求逆矩阵再求原矩阵-对逆矩阵求转置矩阵)- 因为是正交矩阵
- 所以对视图矩阵求逆就是求其转置
summary
Transform objects together with the camera
Until camera’s at the origin, up at Y, look at -Z
Also known as ModelView Transformation 模型视图变换
Projection transformation
- 正交投影(平行光 平截头体)
- 平行的线永远平行
- 透视投影(点光源 锥形体)
- 平行的线会相交
- 近大远小
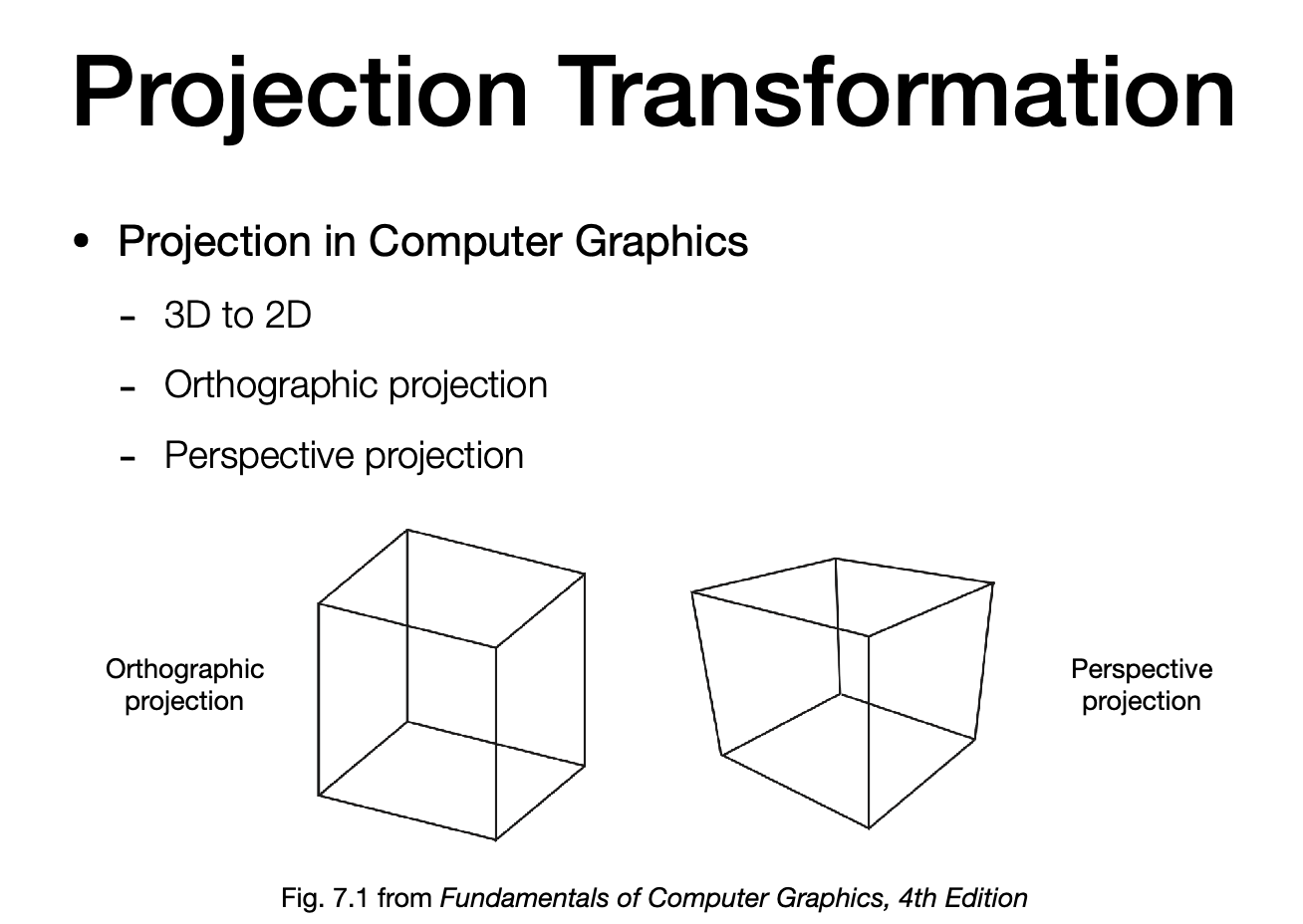
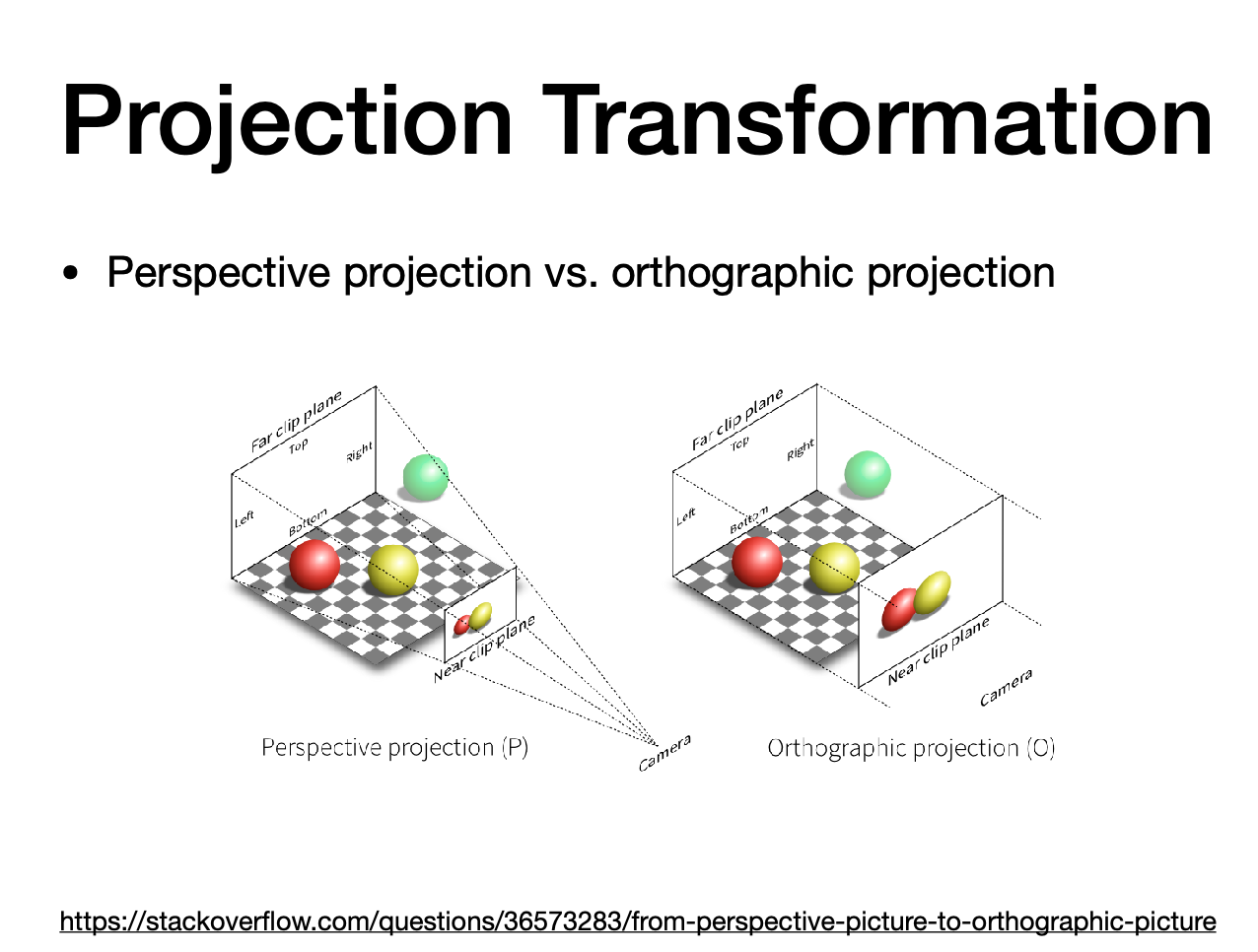
Orthographic projection 正交投影
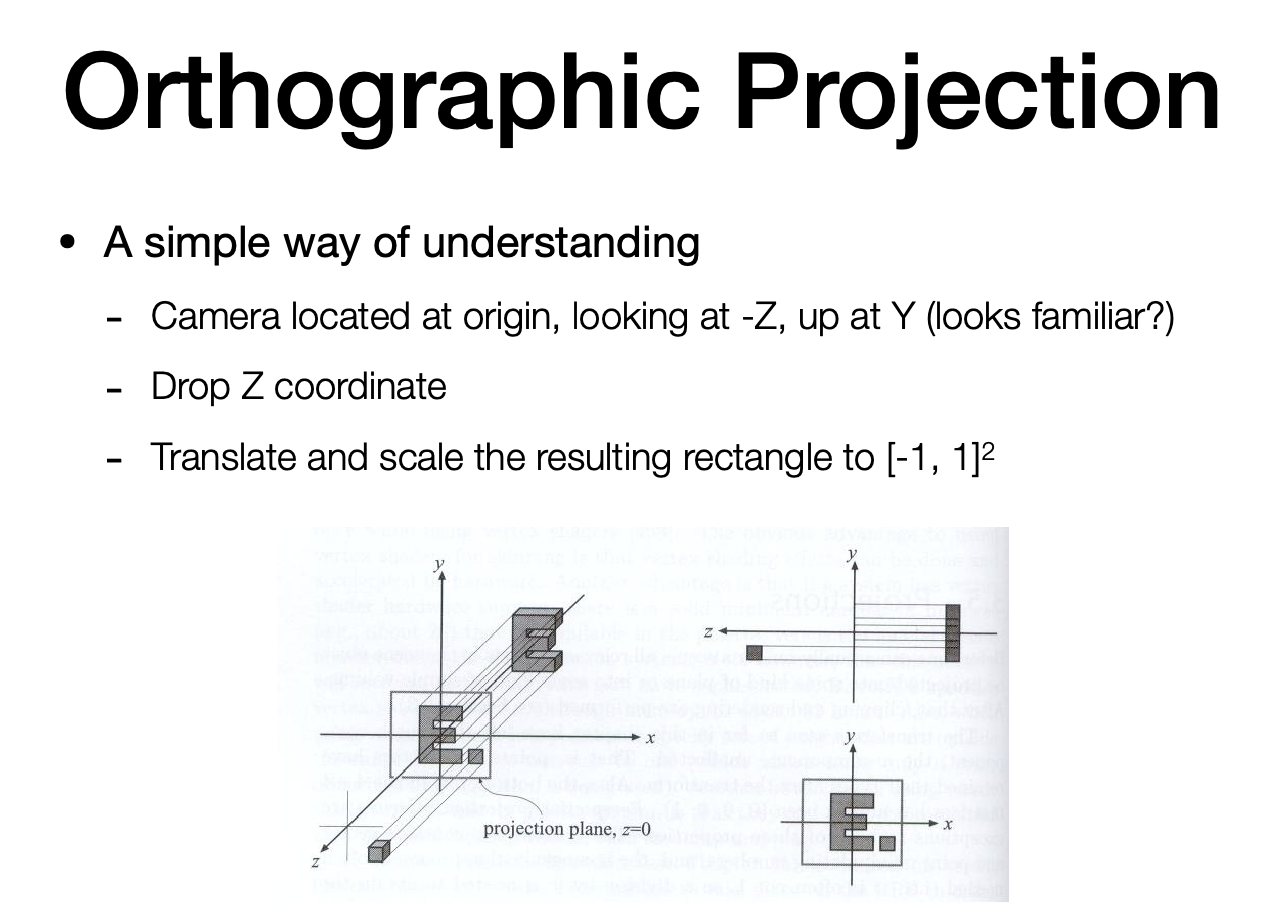
A simple way of understanding
- Camera located at origin, looking at -Z, up at Y (looks familiar?)
- Drop Z coordinate
- Translate and scale the resulting rectangle to $[-1, 1]^2$
In general
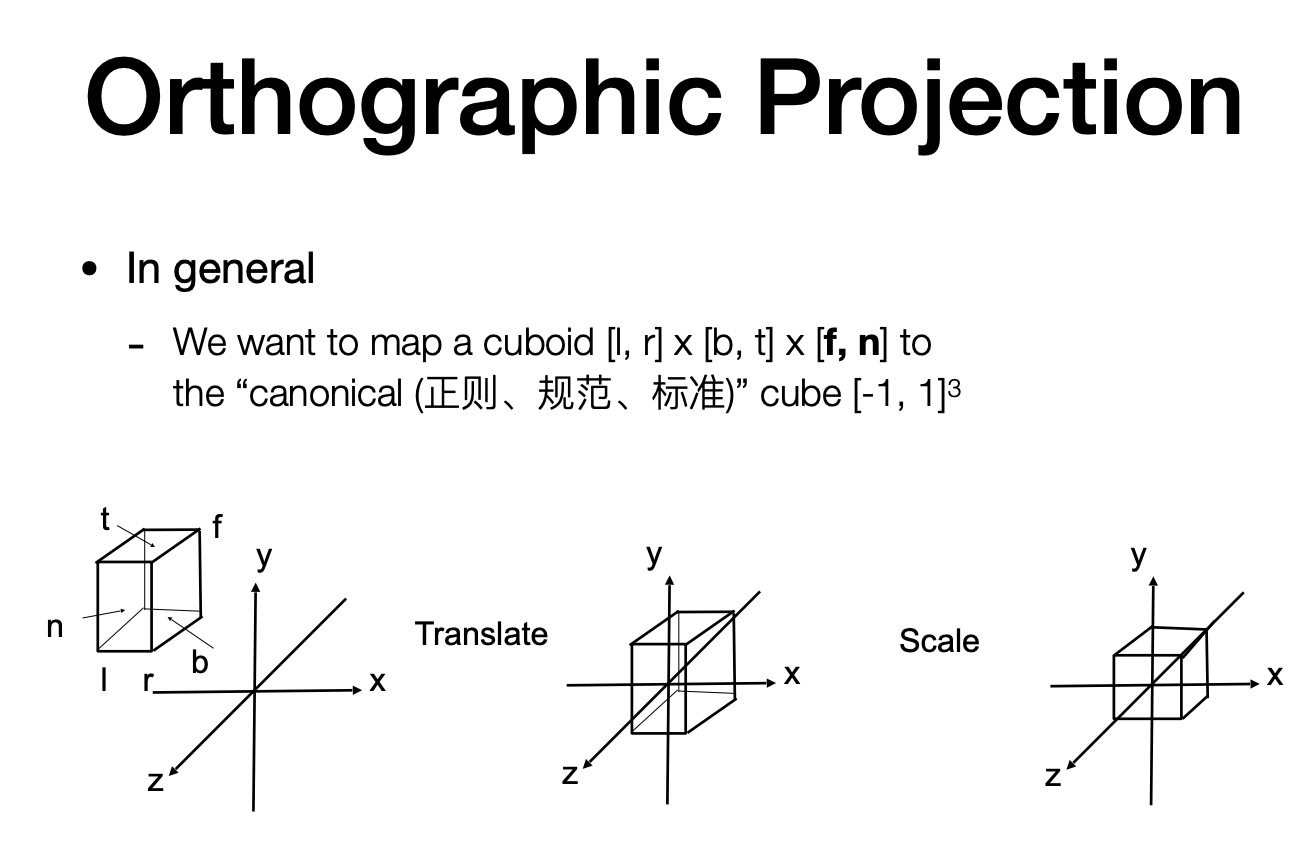
We want to map a cuboid [I, r] x [b, t] x [f, n] to
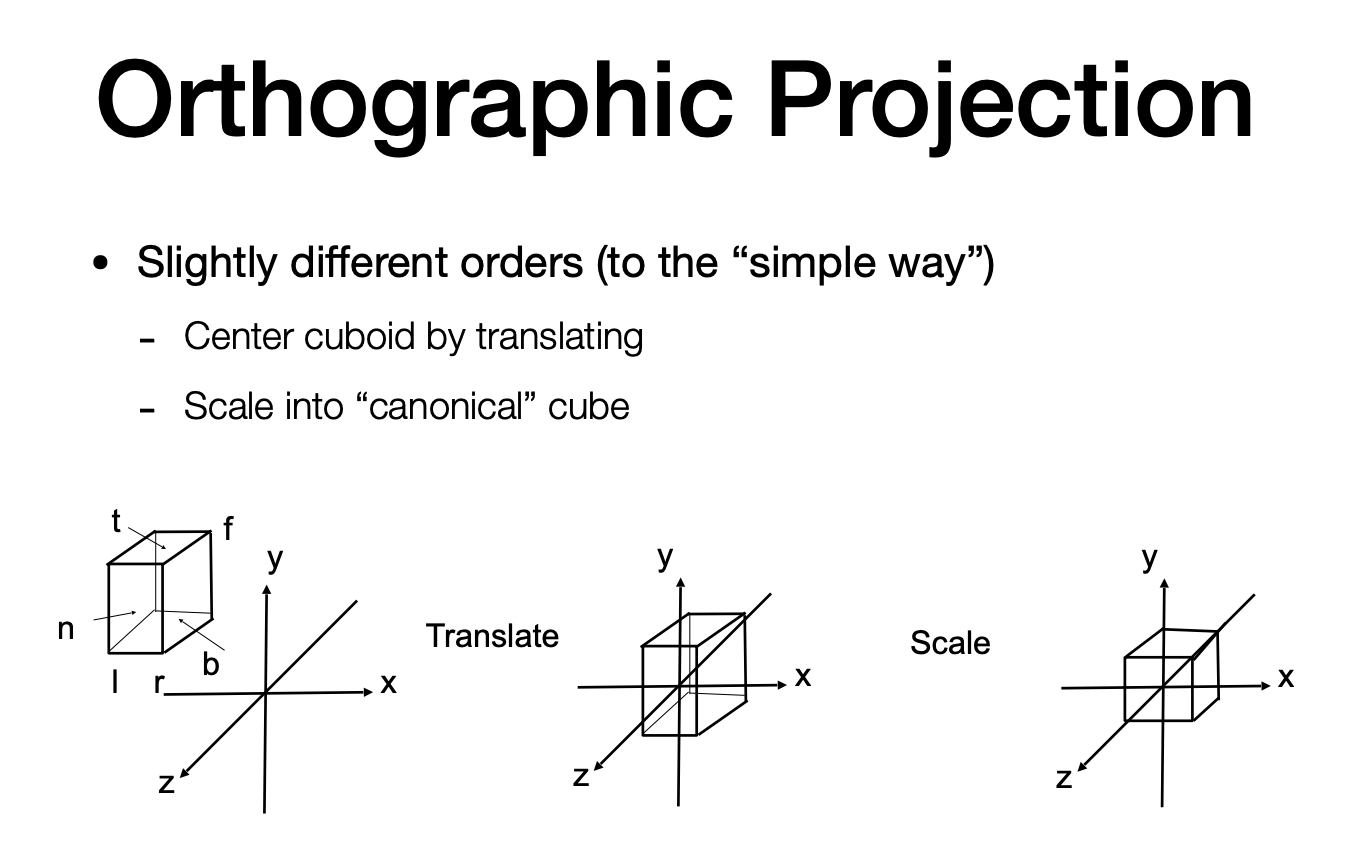
the “canonical ( 正 则 、 规 范 、 标 准 )“ cube $[-1, 1]^3$Slightly different orders (to the “simple way”)
Center cuboid by translating
Scale into “canonical” cube
Transformation matrix
先将各方向的中心平移到原点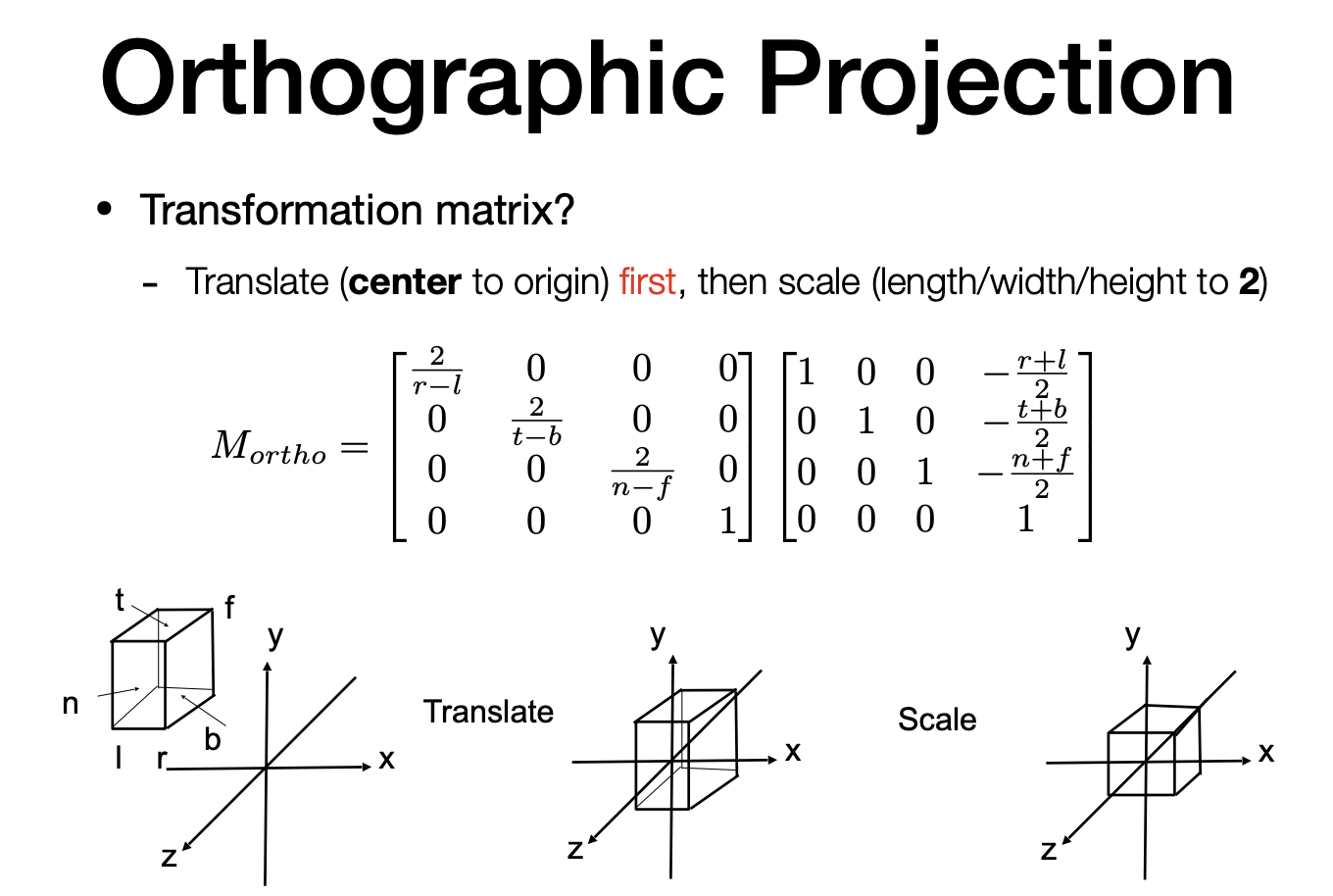
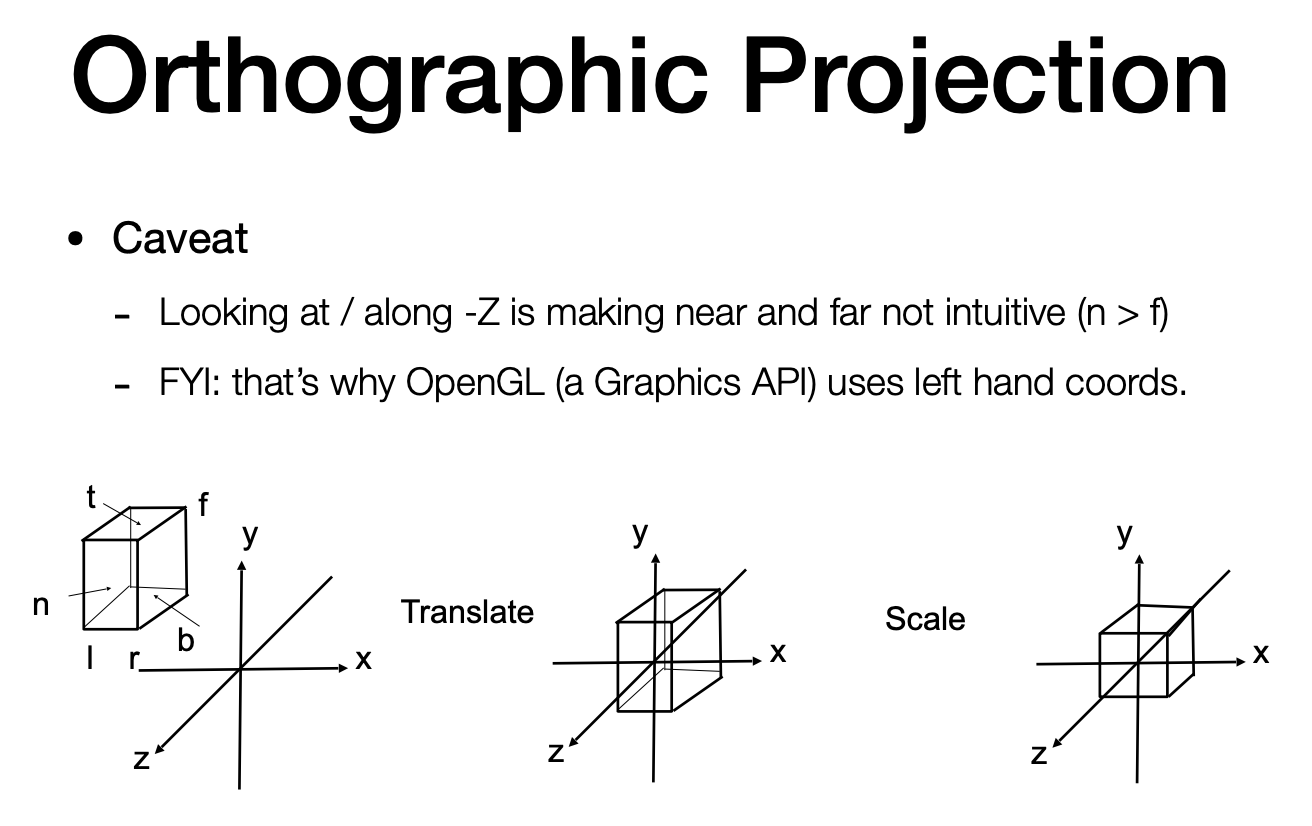
Caveat
- Looking at / along -Z is making near and far not intuitive (n > f)
- FYI: that’s why OpenGL (a Graphics API) uses left hand coords. (观测方向为 z 方向:n 为正的 f 为负的 n > f, -z 方向:n 为负的 far 为正的 n < f)
Perspective projection 透视投影 近大远小
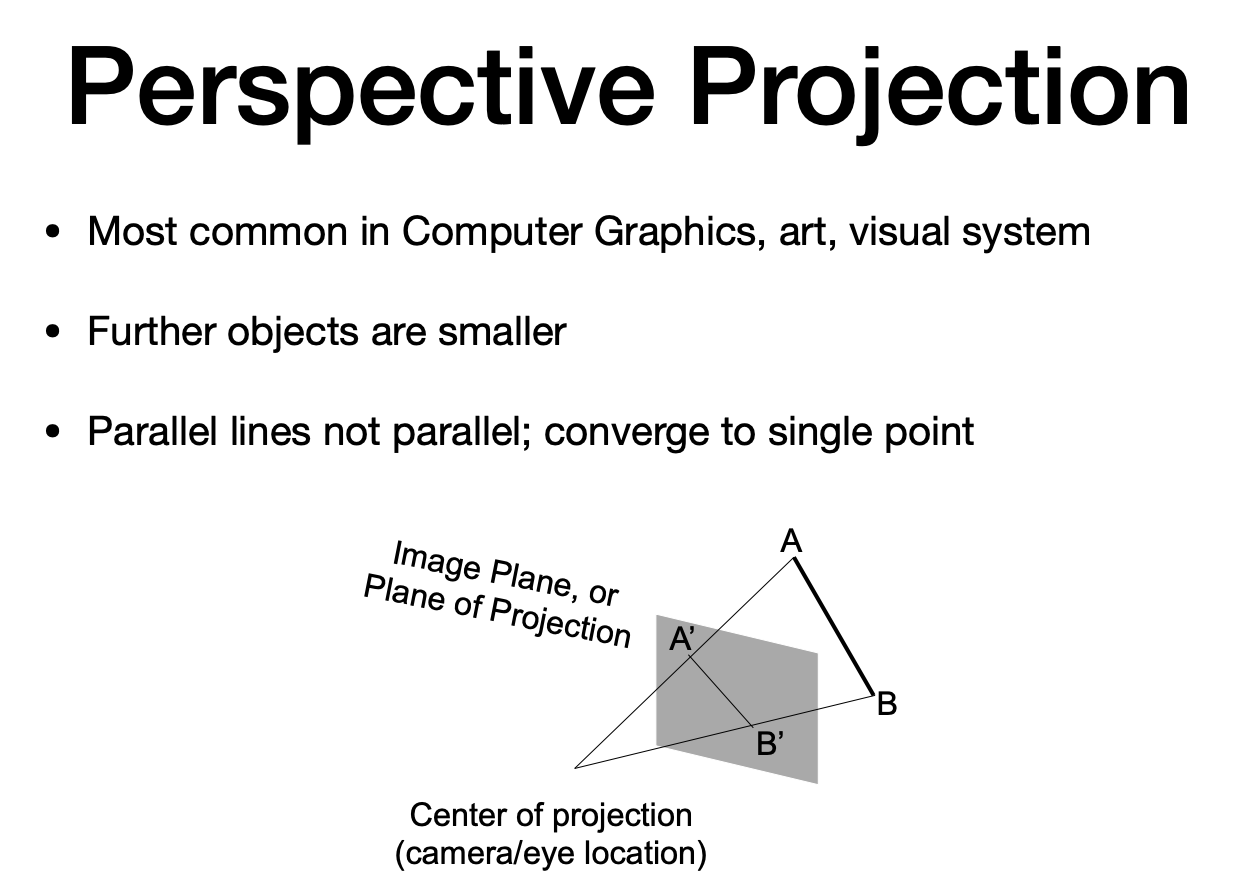
Most common in Computer Graphics, art, visual system
Further objects are smaller 近大远小
Parallel lines not parallel; converge to single point
Euclid
- 平行线永不相交
- 但透视投影中会相交
Before we move on
Recall: property of homogeneous coordinates
- (x,y,z,1), (kx, ky, kz, k != 0), (xz, yz, $z^2$, z != 0) all represent the same point (x, y, z) in 3D
- e.g. (1, 0, 0, 1) and (2, 0, 0, 2) both represent (1, 0, 0)
- (x,y,z,1), (kx, ky, kz, k != 0), (xz, yz, $z^2$, z != 0) all represent the same point (x, y, z) in 3D
Simple, but useful
How to do perspective projection
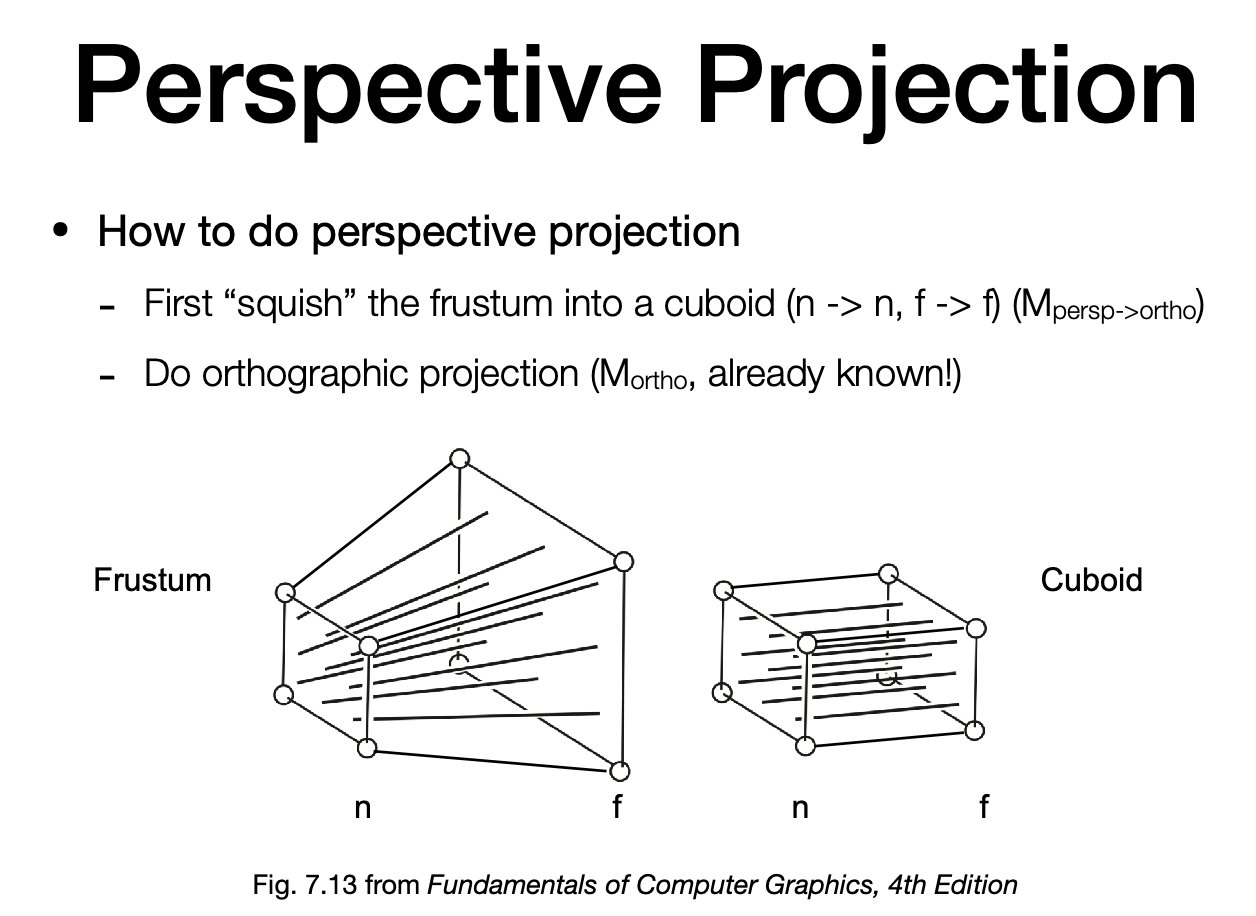
- 把透视投影分解为两步骤
- 1.挤压成长方体
- 2.进行正交投影
- 如何挤压
- 原则
- 近平面永远不变
- 挤了之后各自平面z不变
- 远平面中心点挤后不变
- 任何一个点变换前后z不变
- 中间一个点经过挤压后如何变化
- 原则
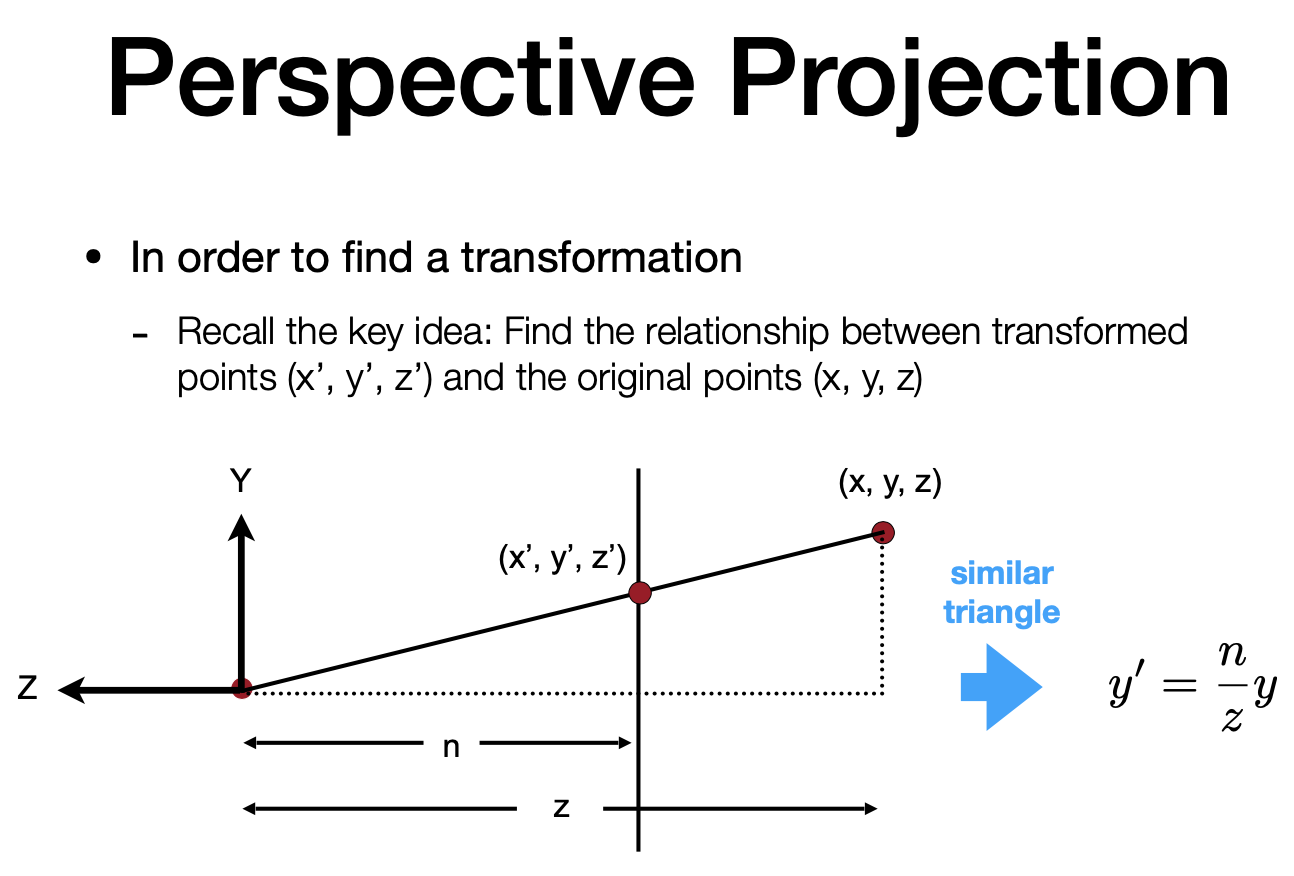
- 相似三角形
- y’ 和 y 的关系 $y’ = \frac{n}{z}y$
- x’ 和 x 的关系 $x’ = \frac{n}{z}x$ (与 y 同理)
- 把透视投影分解为两步骤
齐次坐标下乘以一个非零数 k 依然为原来那个点(都乘 z)
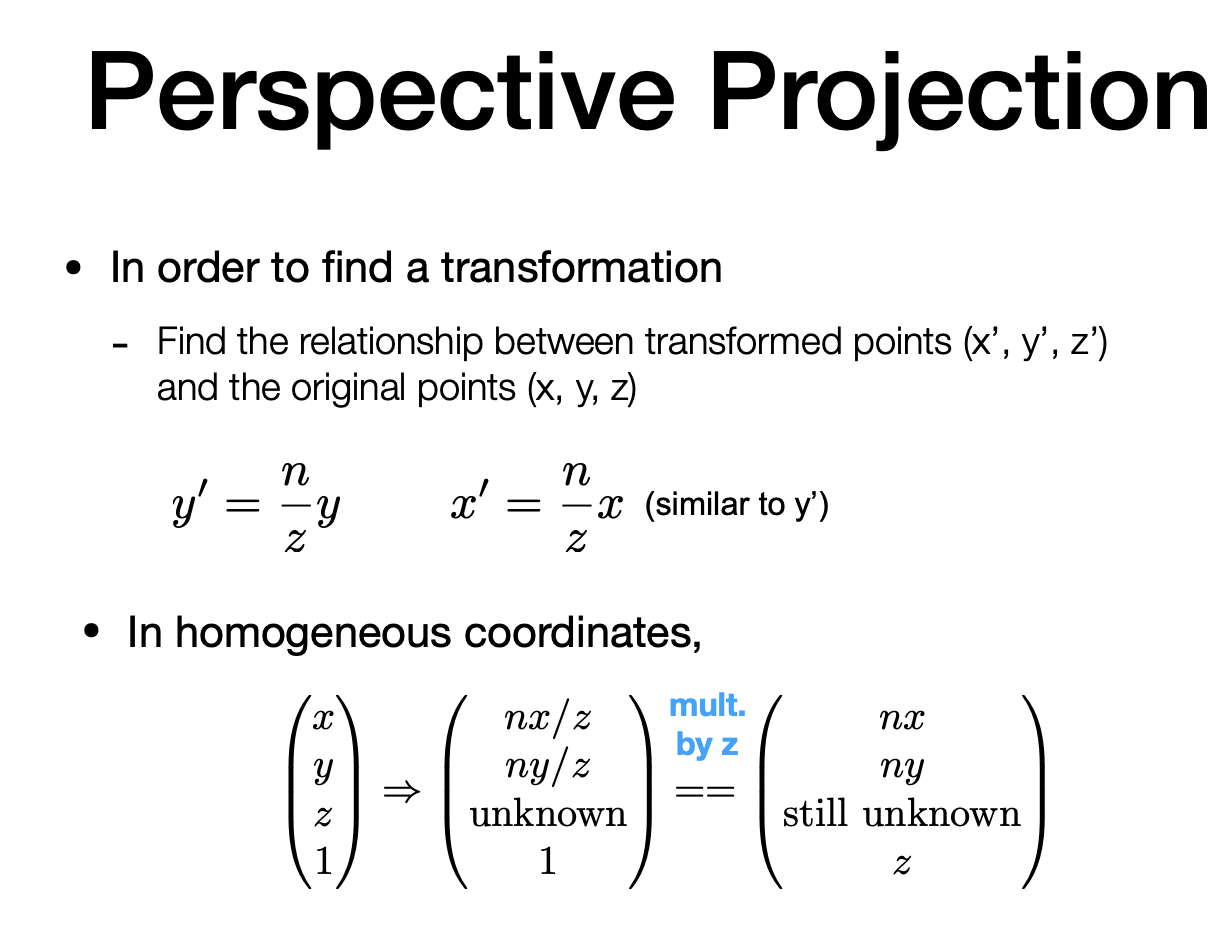
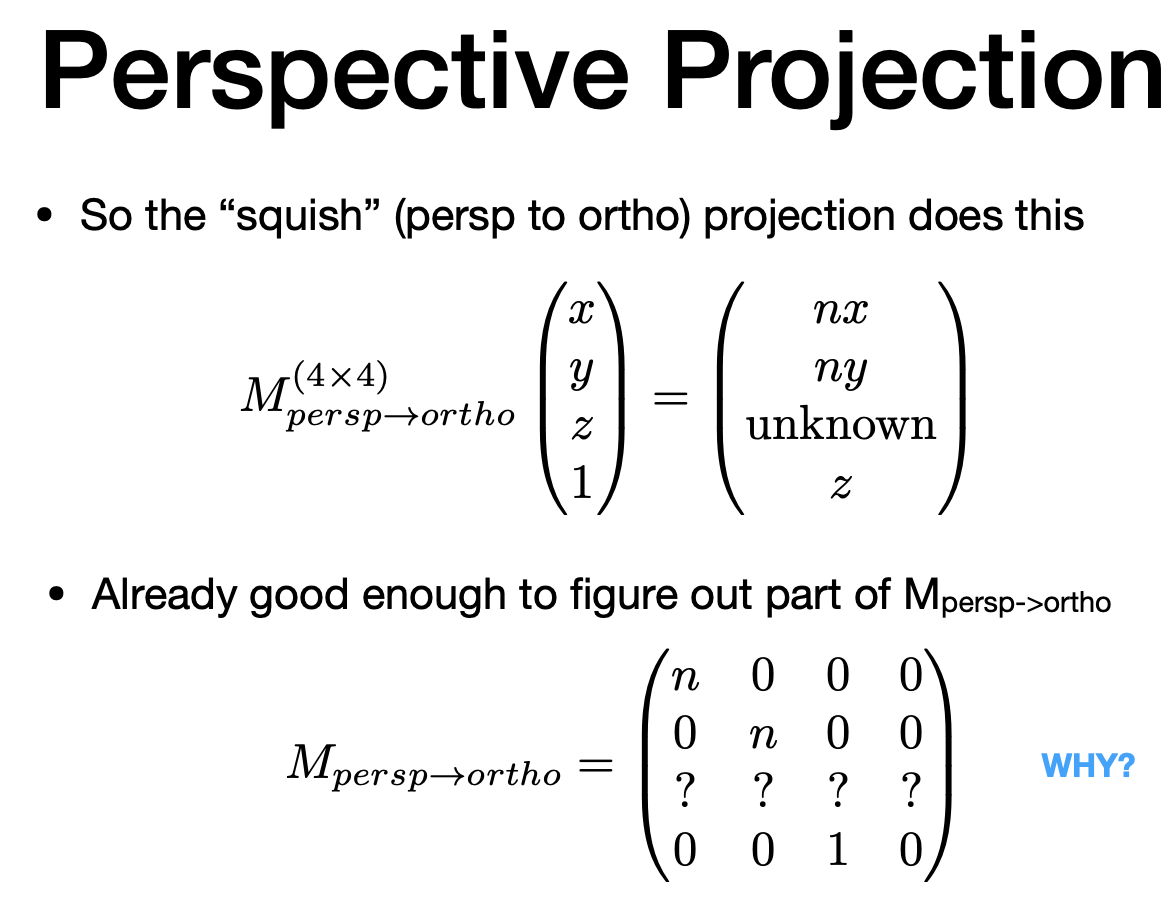
如何求剩余矩阵
两个观察
1.近平面上任意点都不会变
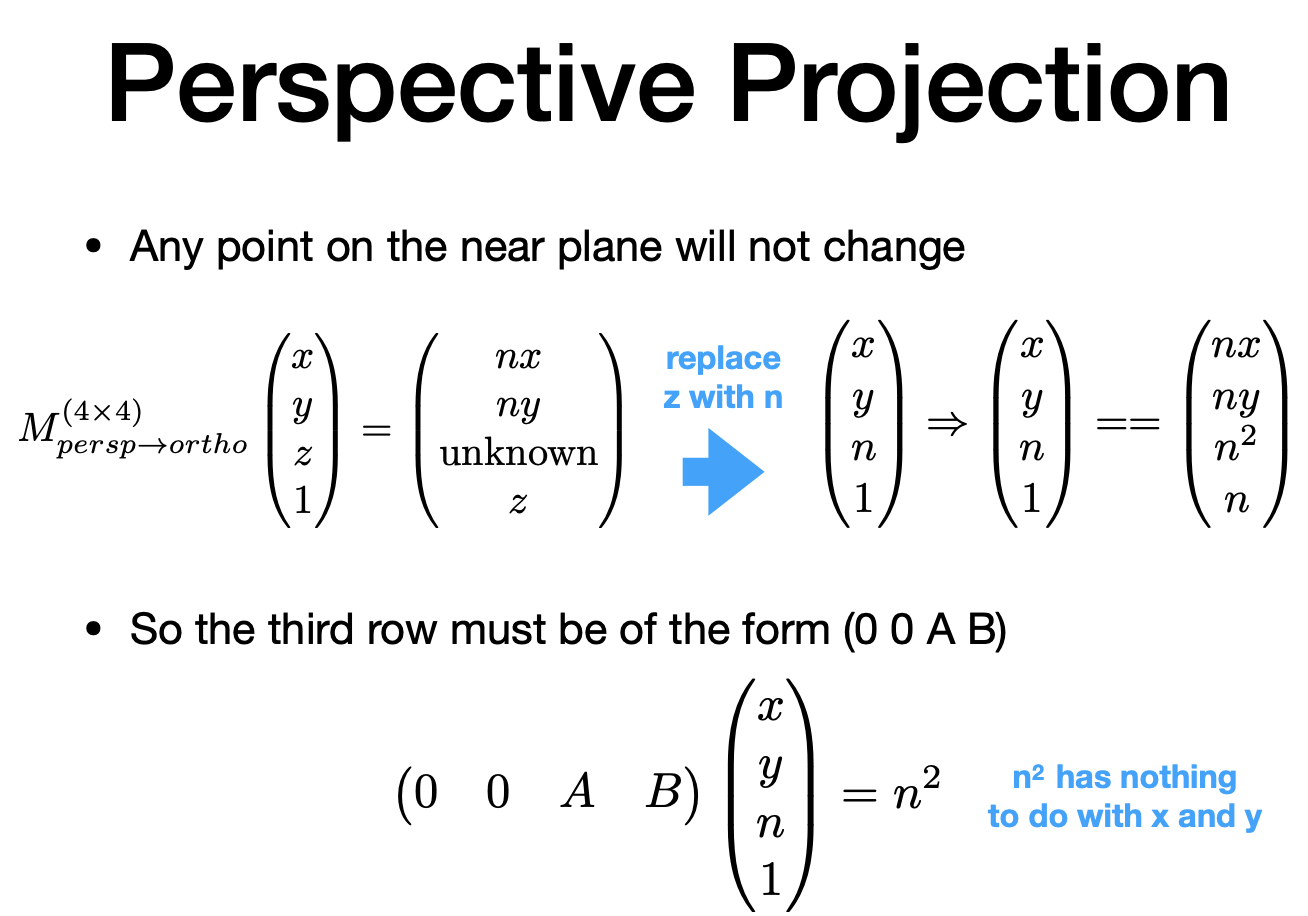
$n^2$和 x y 无关
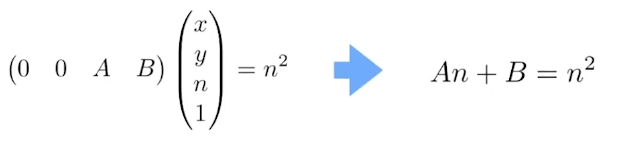
2.远平面上任意点的 z 不会变

取远平面中心点

求解方程之后可知 AB,则 $M_{persp \rightarrow ortho}$ 得解