GAMES101-3 20200218 20210704 Transformation

3 20200218 / 20210704 Transformation

Why study transformation

• type
  • Modeling 模型变换
    • 摄像机移动
    • rotation
    • scaling 皮克斯动画
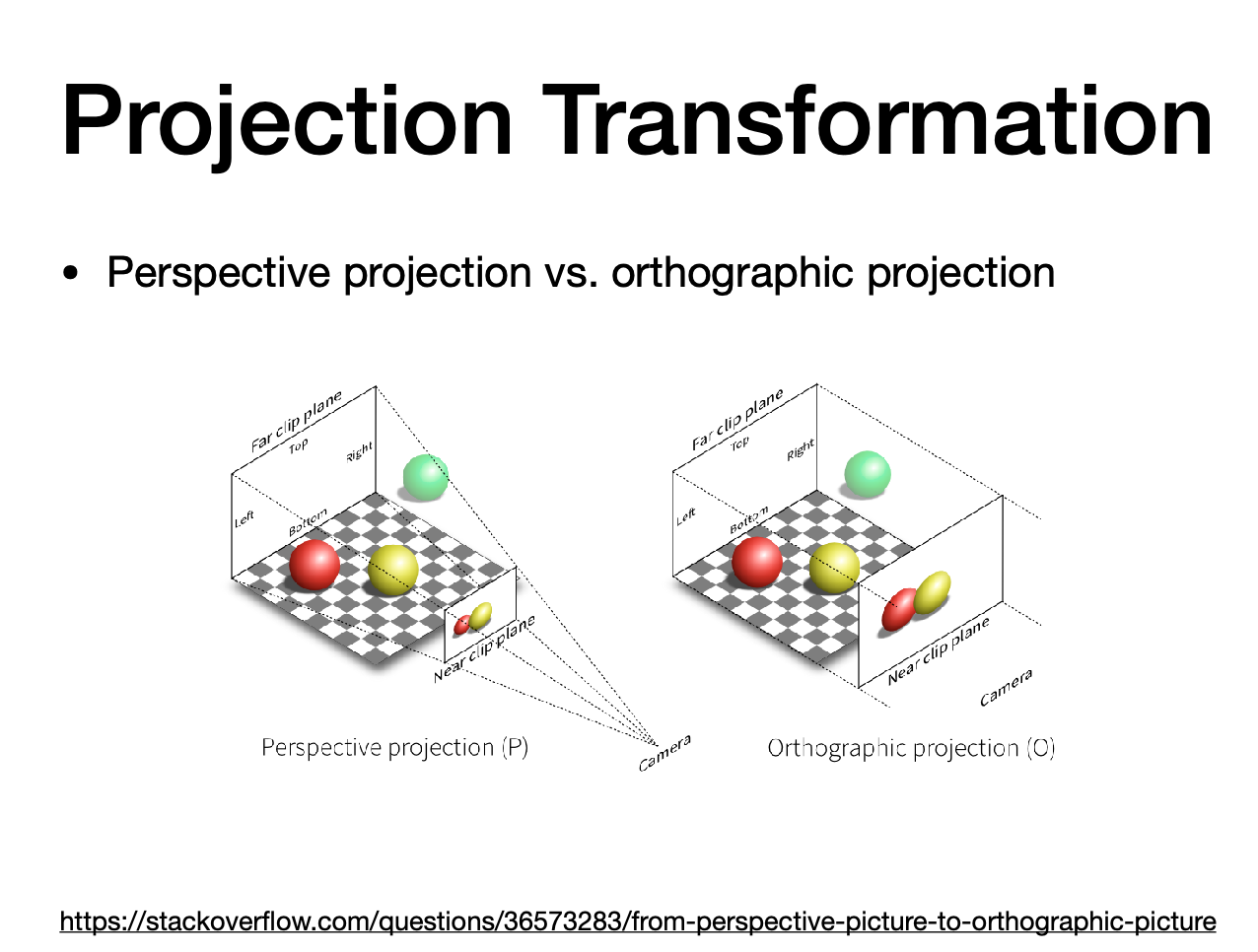
  • Viewing 视图变换 （3D to 2D projection）
    • 光栅化
    • 投影
• 2D transformations
• Homogeneous coordinates

2D transformations

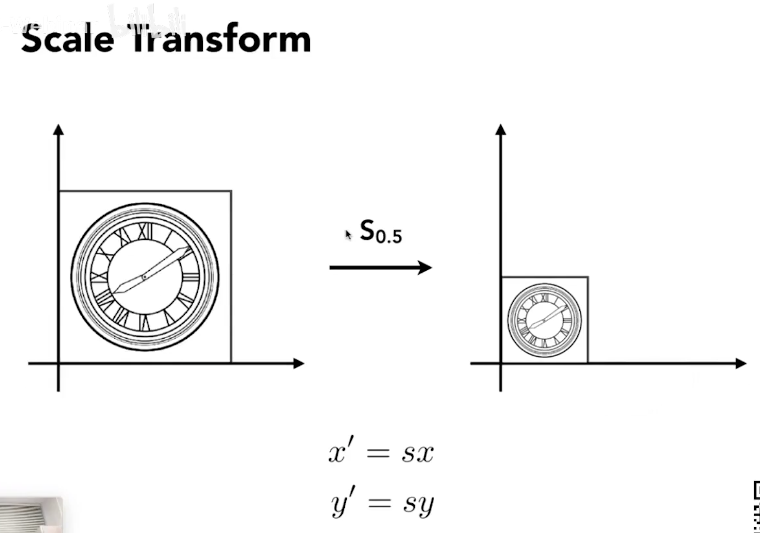
Scale

• uniform ($S_{0.5}$)

  

  • scale matrix

    

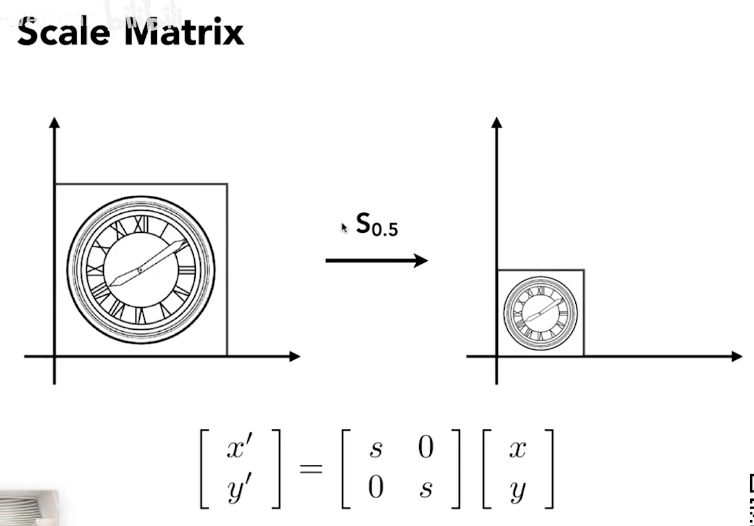
• non-uniform

  

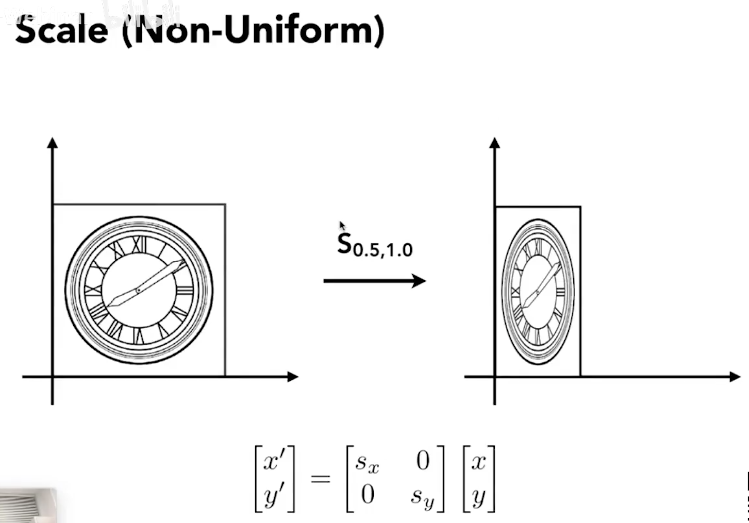
Reflection Matrix

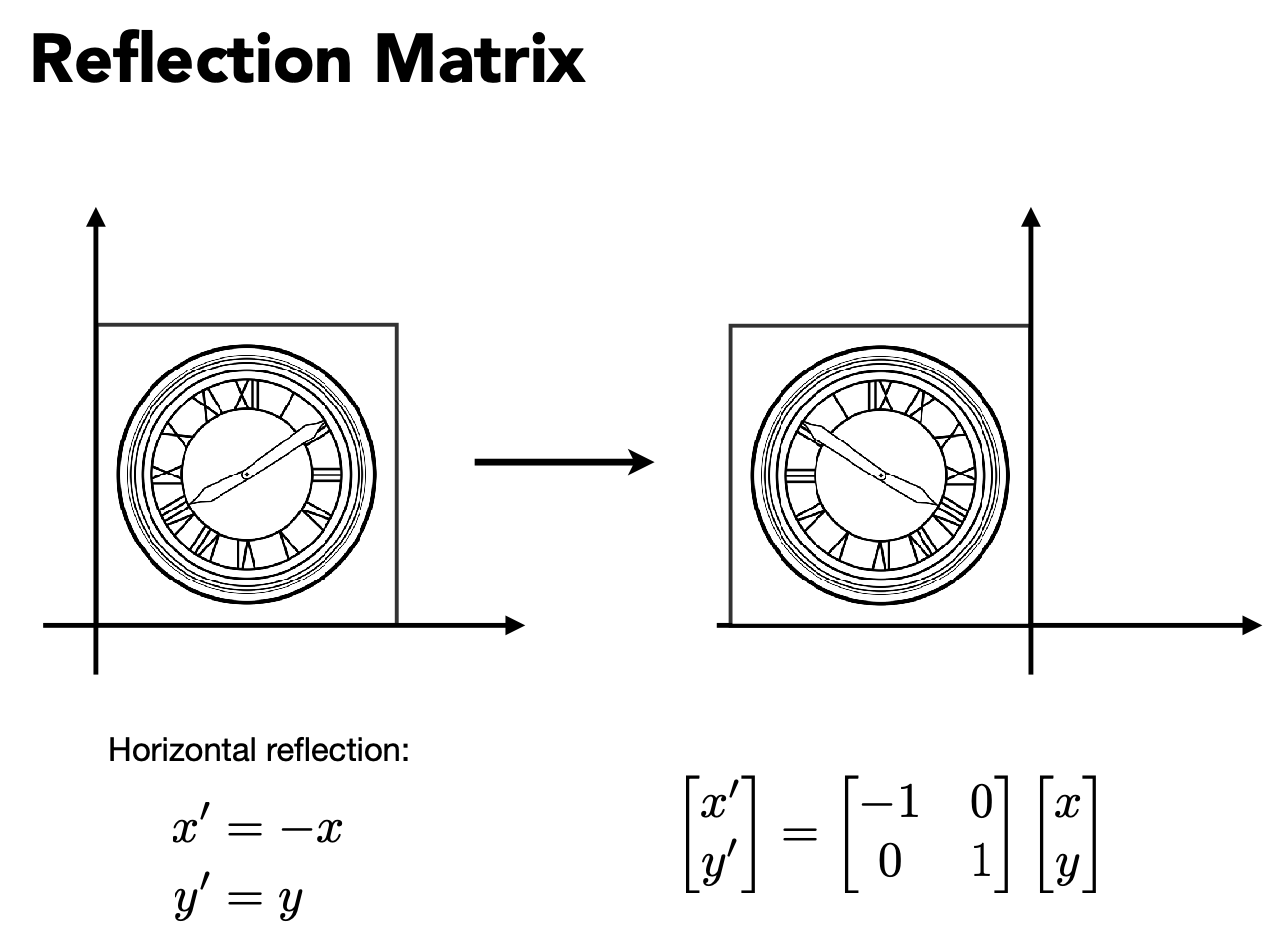
Shear Matrix 错切

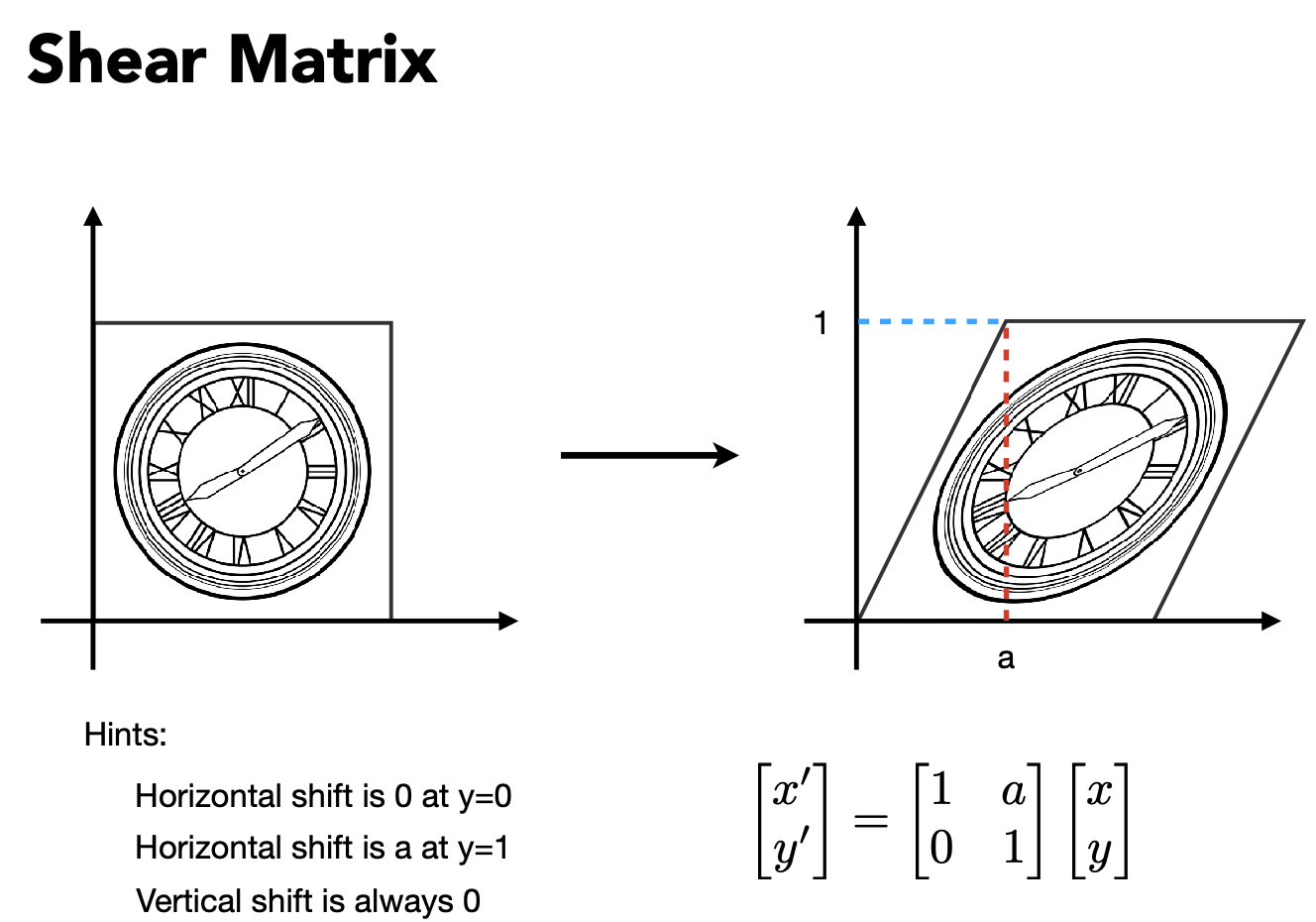
Rotate 围绕(0,0)逆时针

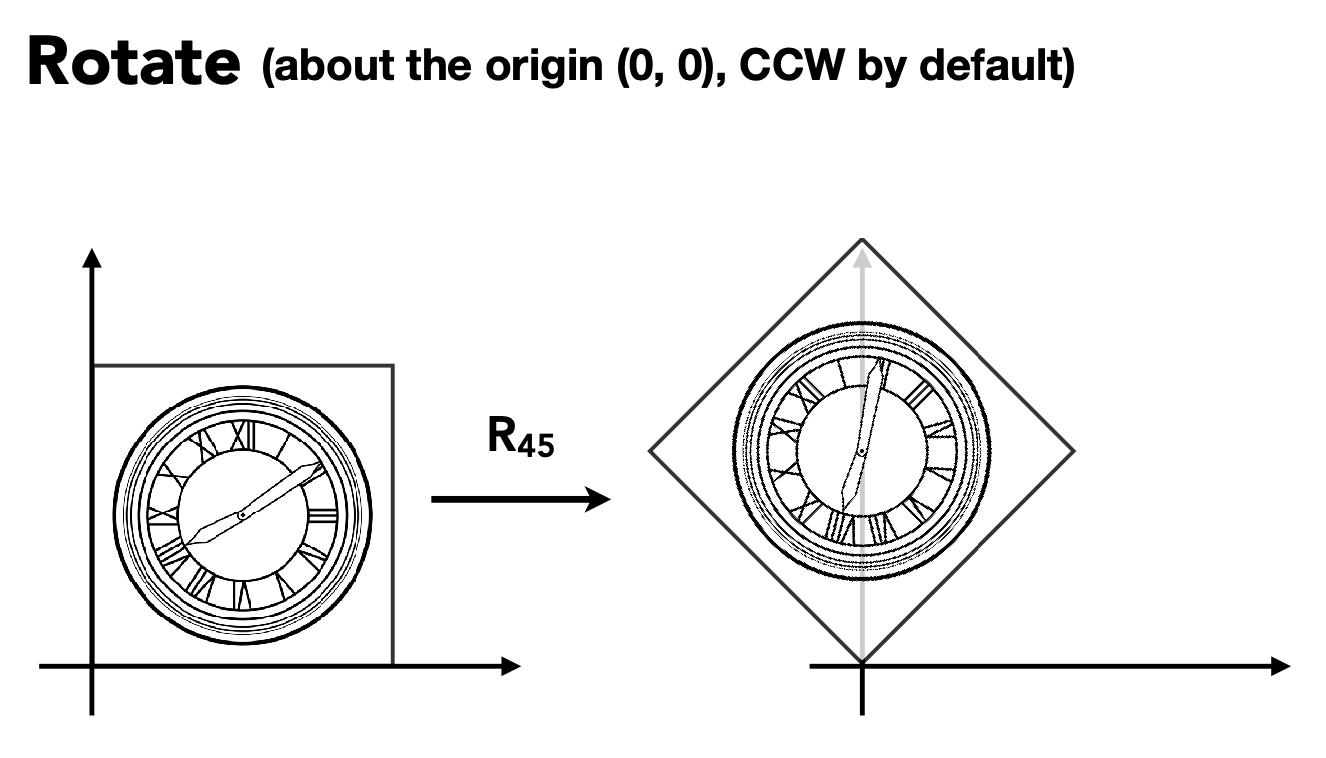
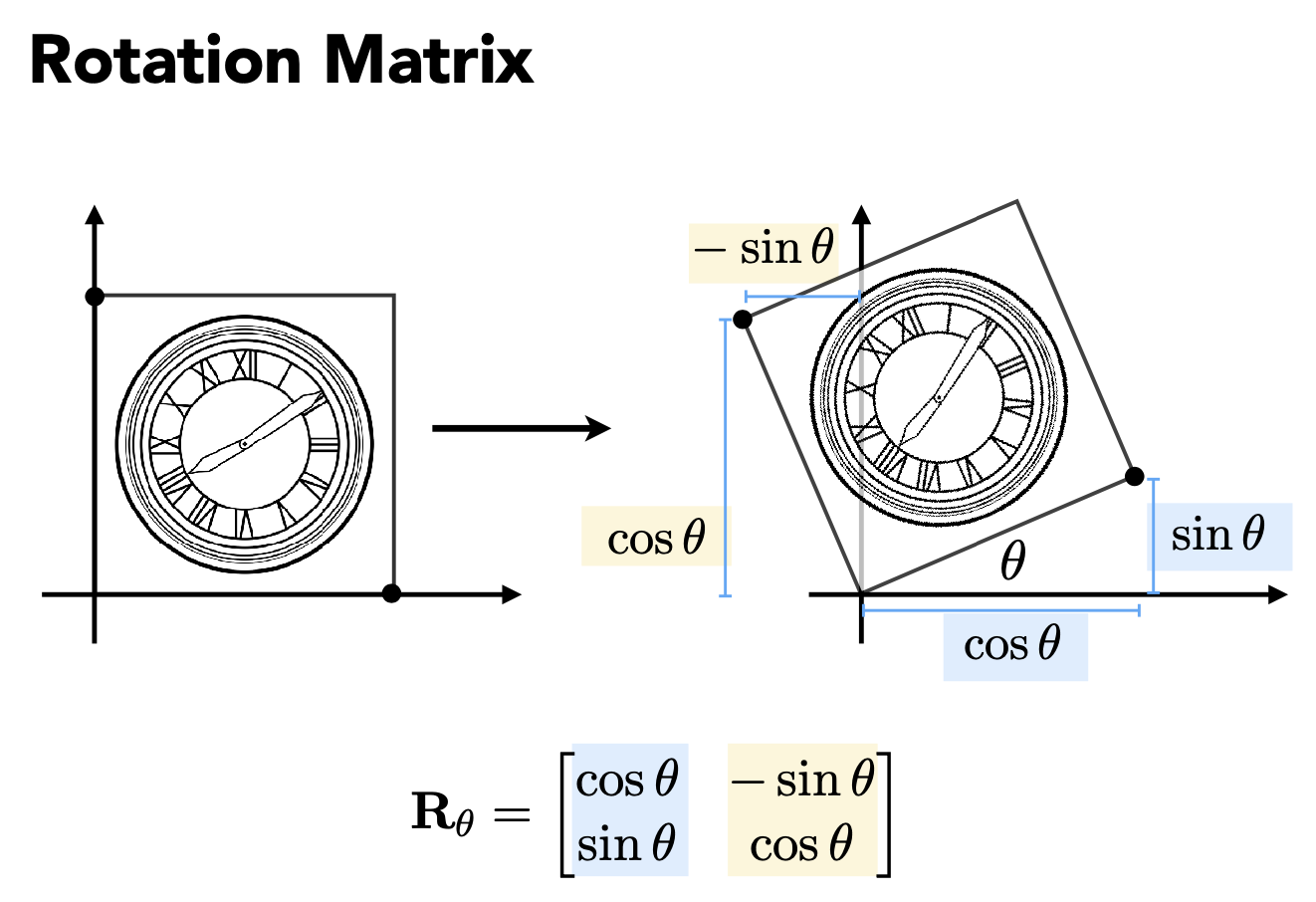
Linear Transforms = Matrices

Homogeneous coordinates

• why

低一维的加法可以用高一维的乘法替换，所以有了齐次坐标目的：用齐次坐标统一所有变换 trade-off

平移变换

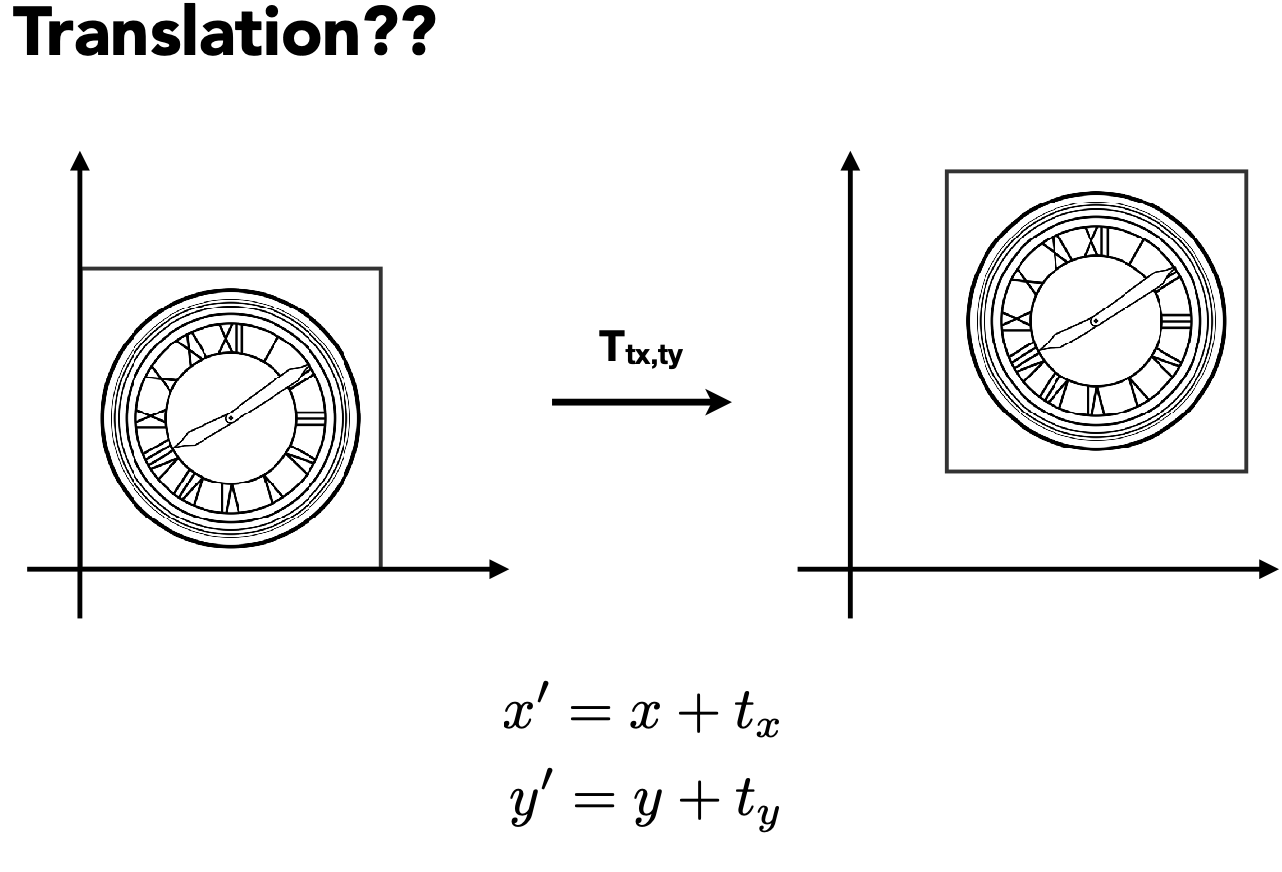
向量具有平移不变性

point + point = 两点中点

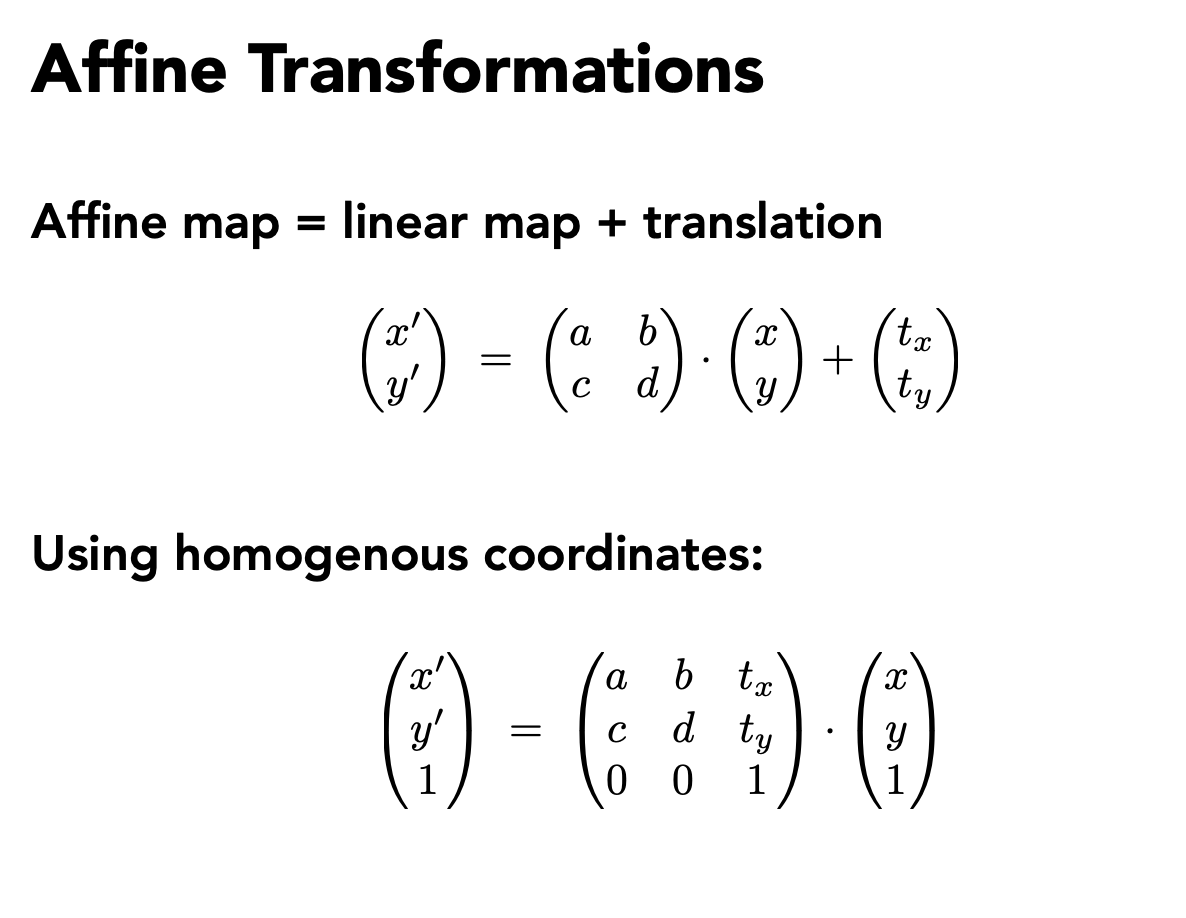
Affine Transformations 仿射变换 （线性变换（左上角矩阵）+平移变换（最后一列））

• 先线性变换再平移

  

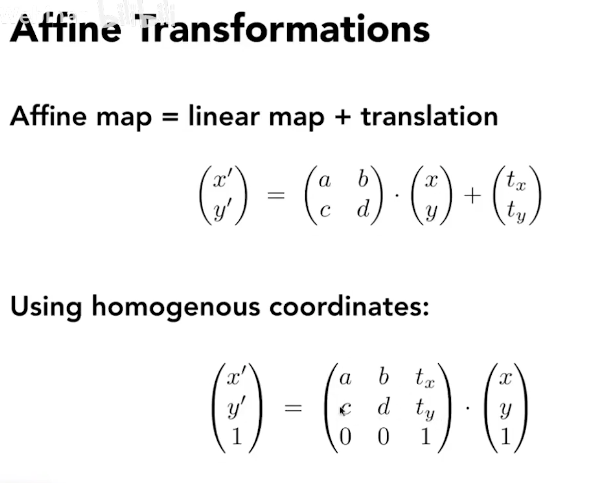
2D Transformations

只有二维情况下仿射变换最后一行才是 001

Inverse Transform 逆变换

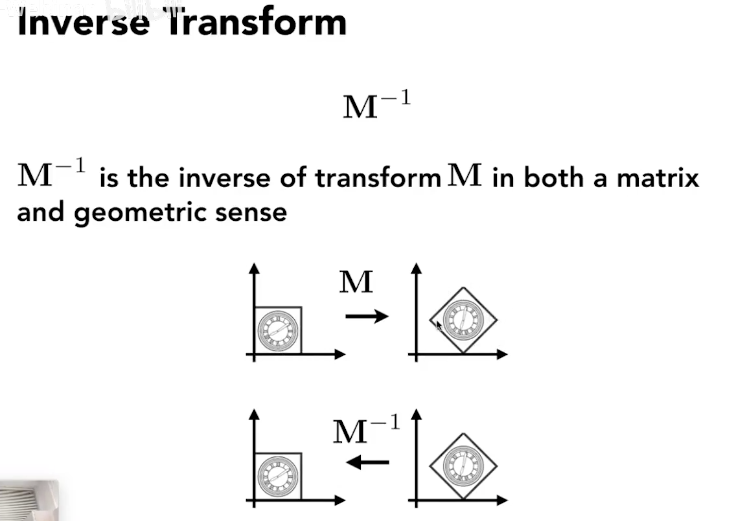
Composing Transform 组合变换

• 复杂变换可通过简单变换得到

• 变换的顺序很重要（矩阵乘法不满足交换律）

  

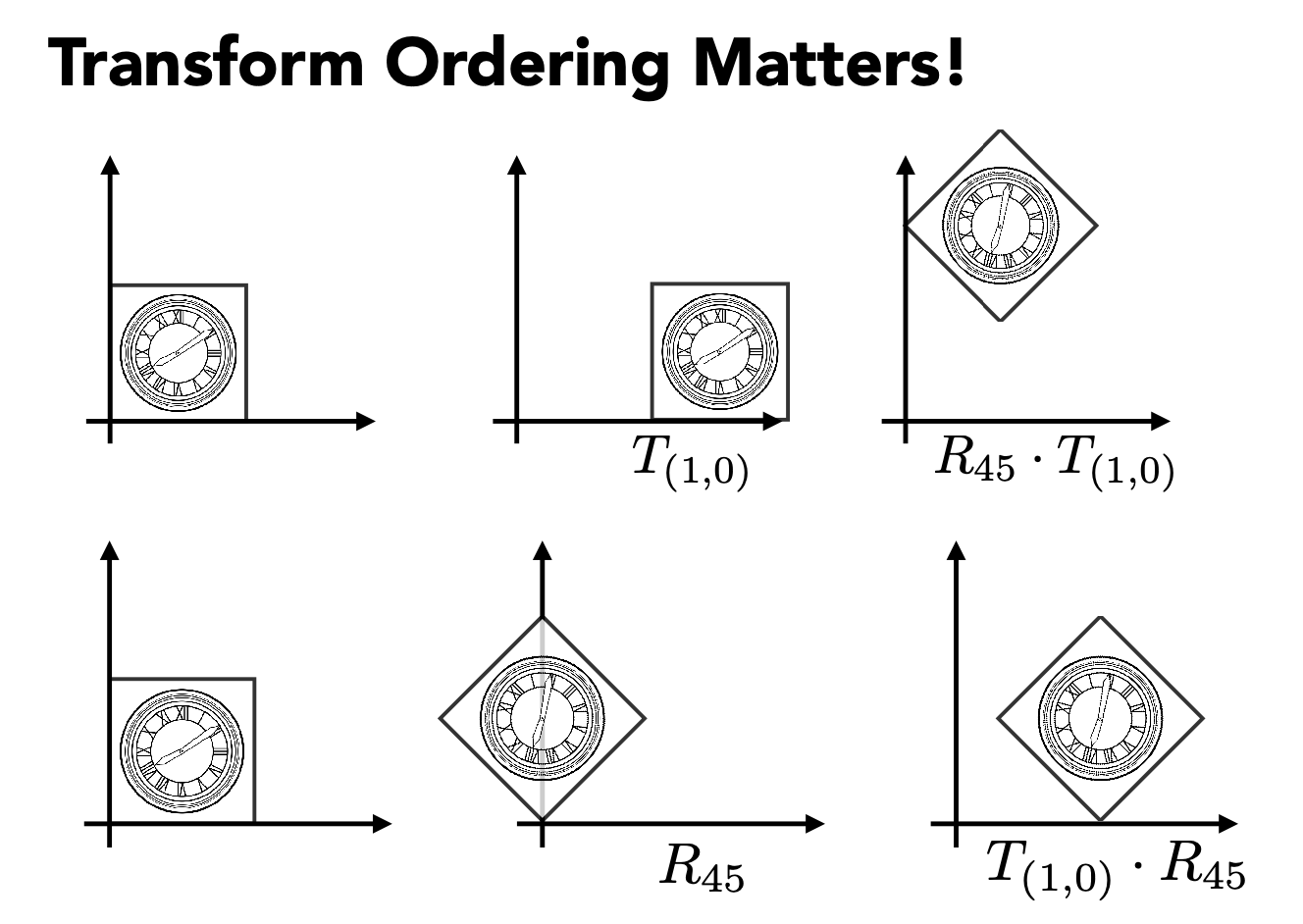
• 矩阵放左边*向量

• 矩阵变换从右至左应用

• 矩阵没交换律但有结合律

  

• 可用一个矩阵表述非常复杂的变换

Decomposing Complex Transfroms 分解复杂矩阵

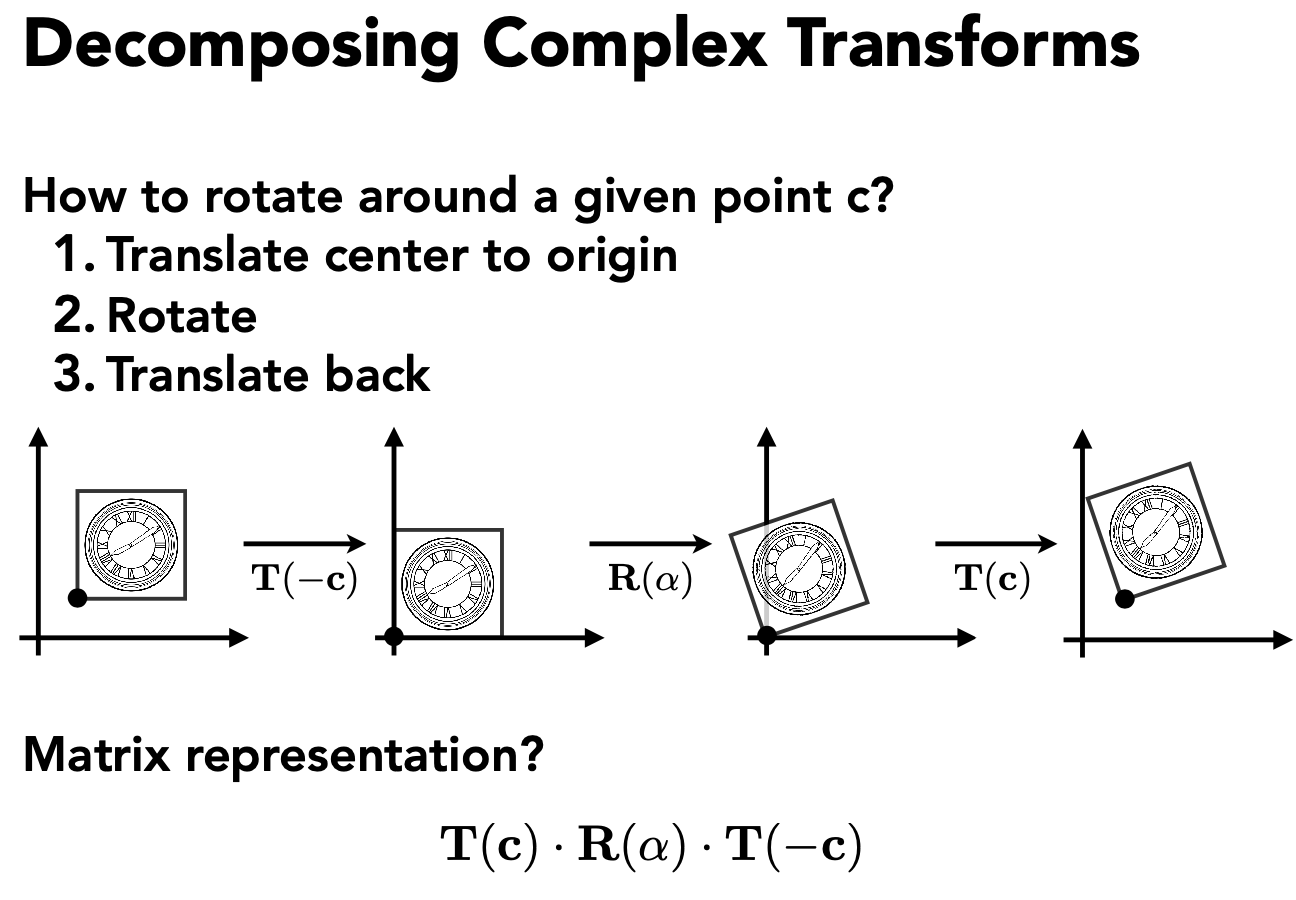
• 想要以某点为中心进行旋转
  • 先将该点移动到原点 - T(-c)
  • 进行旋转 - R (a)
  • 然后再逆操作移动到原位置 - T(c)
  • $T(c) · R(\alpha) · T(-c)$

3D Transforms

和 2D 做类比

• 用四个数表示
  • 点则末尾加 1
  • 向量则末尾加 0

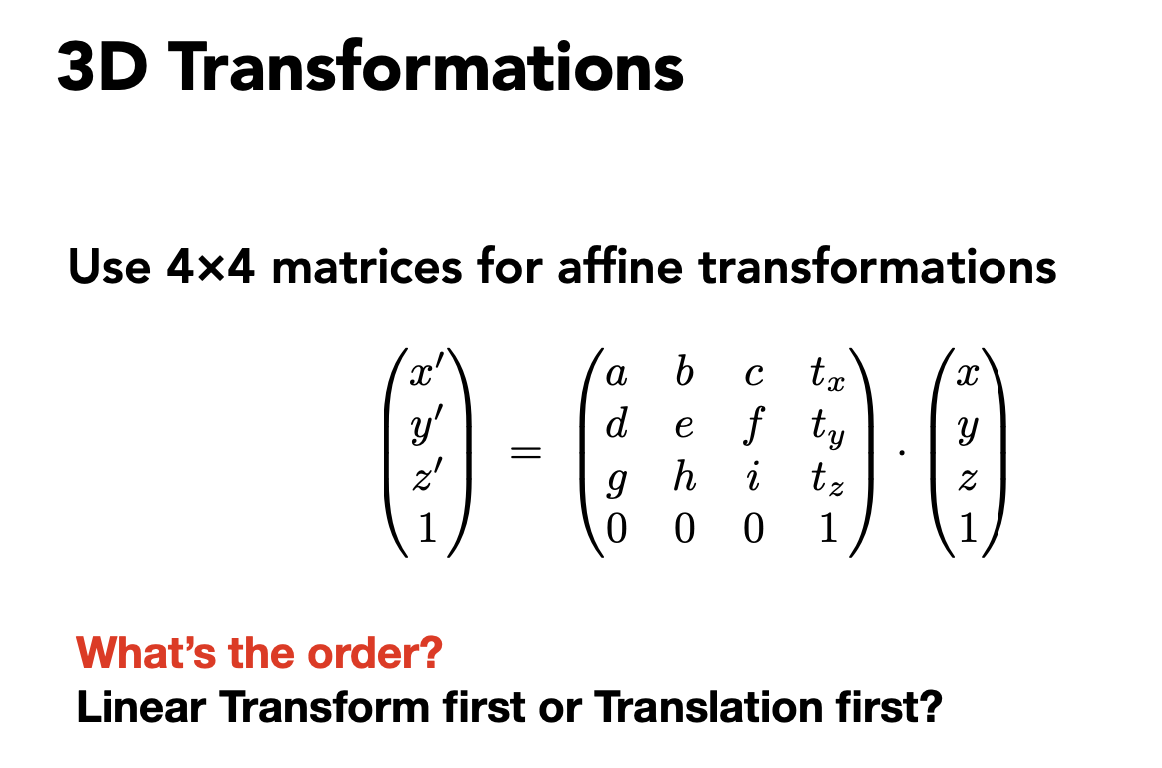
仿射变换 = 线性变换 + 平移变换
先线性变换（缩放/旋转） 再平移变换