GAMES101-2 20200214 20210704 A Swift and Brutal Introduction to Linear Algebra

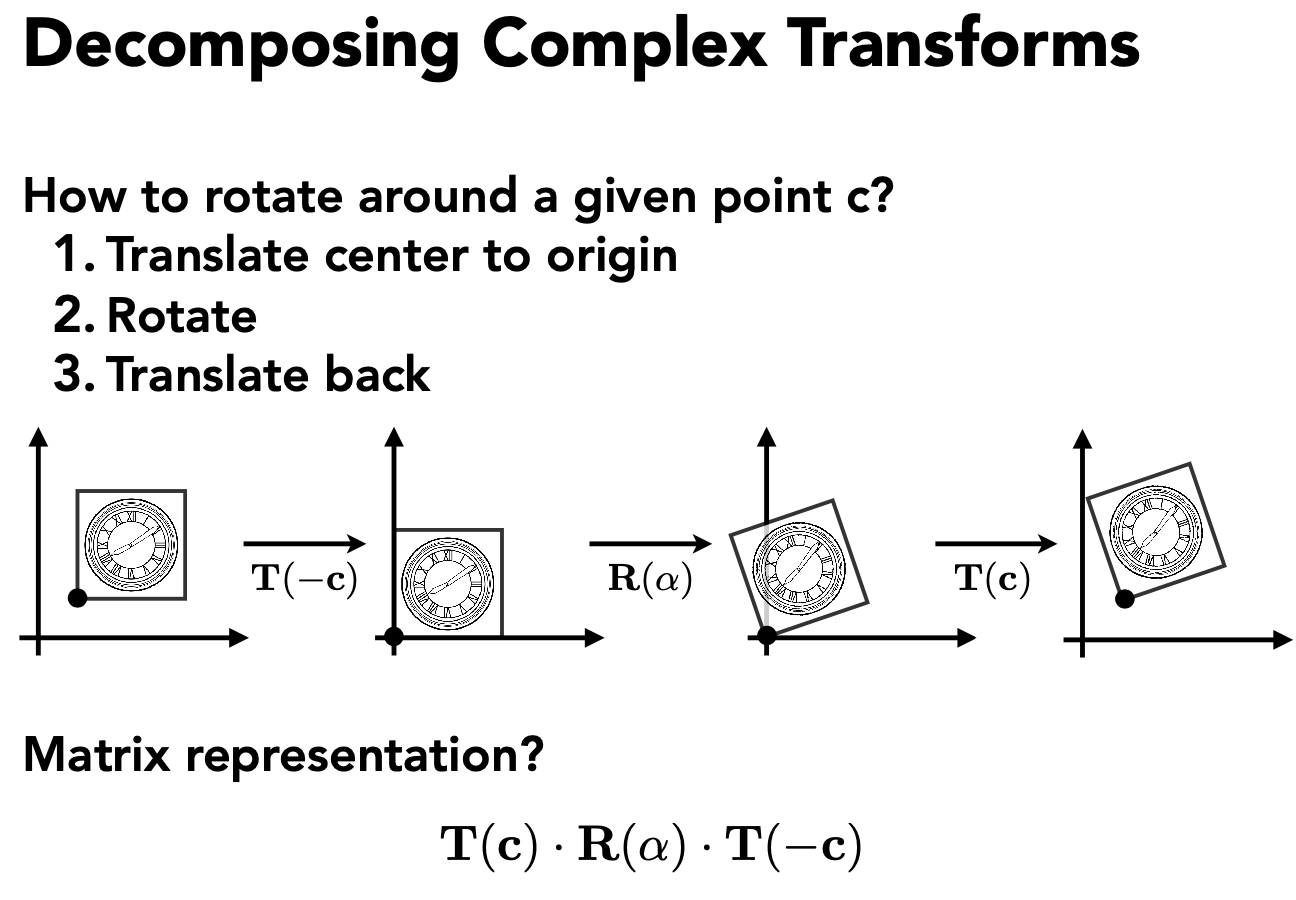
2 20200214 / 20210704 A Swift and Brutal Introduction to Linear Algebra!

(in fact it’s relatively easy…)

• Graphics’ Dependencies
  • Basic mathematics
    • Linear algebra, calculus, statistics
  • Basic physics
    • Optics, Mechanics
  • Misc
    • Signal processing, Numerical analysis
  • And a bit of aesthetics

This Course

• More dependent on Linear Algebra
  • Vectors (dot products, cross products, …)
  • Matrices (matrix-matrix, matrix-vector mult., …)
• For example,
  • Apoint is a vector (?)
  • An operation like translating or rotating objects
    can be matrix-vector multiplication

Vectors

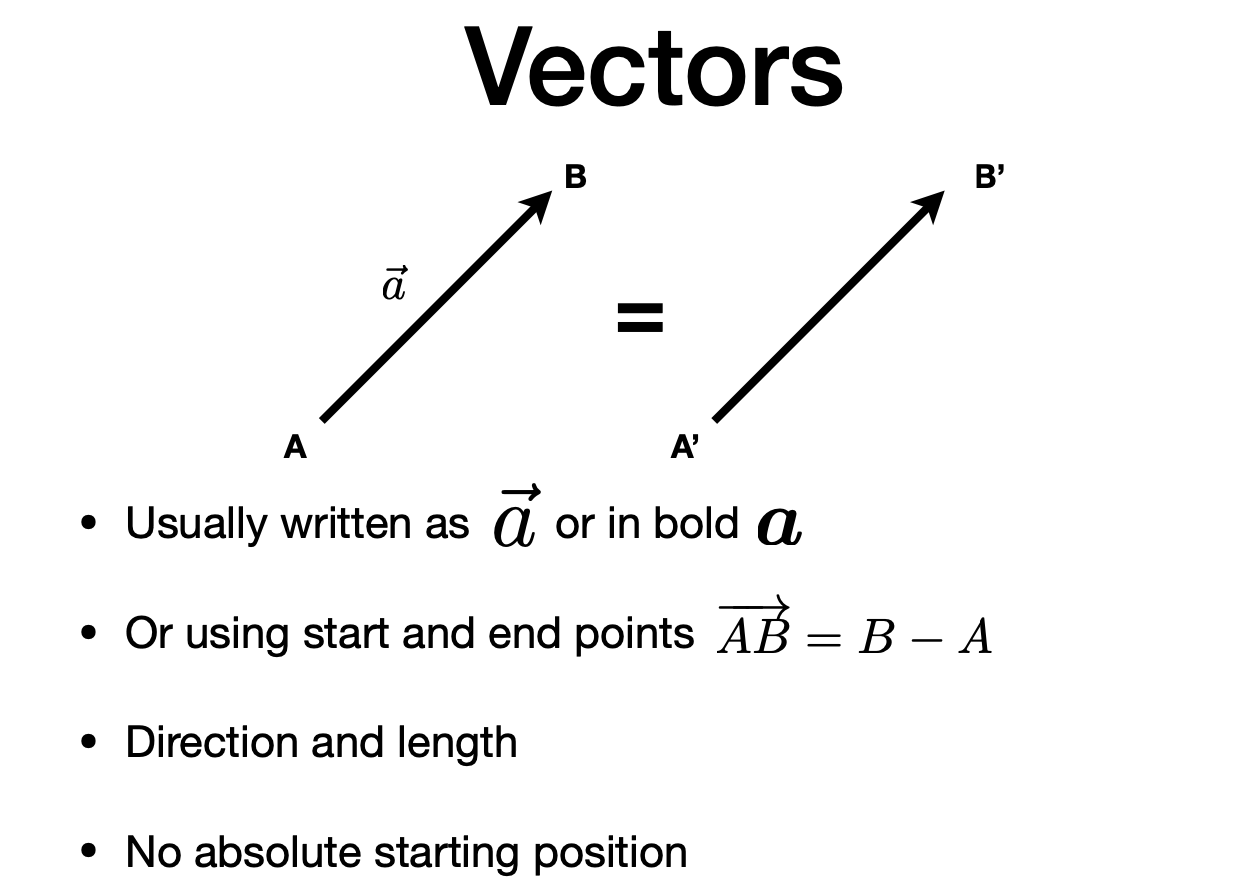
• Usually written as $\vec a$ or in bold $\bf{a}$
• Or using start and end points $\vec{AB}=B-A$
• Direction and length
• No absolute starting position

Vector Normalization

• Magnitude (length) of a vector written as $||\vec a||$
• Unit vector .
  • Avector with magnitude of 1
  • Finding the unit vector of a vector (normalization): $\hat a = \vec a / ||\vec a||$
  • Used to represent directions

Vector Addition

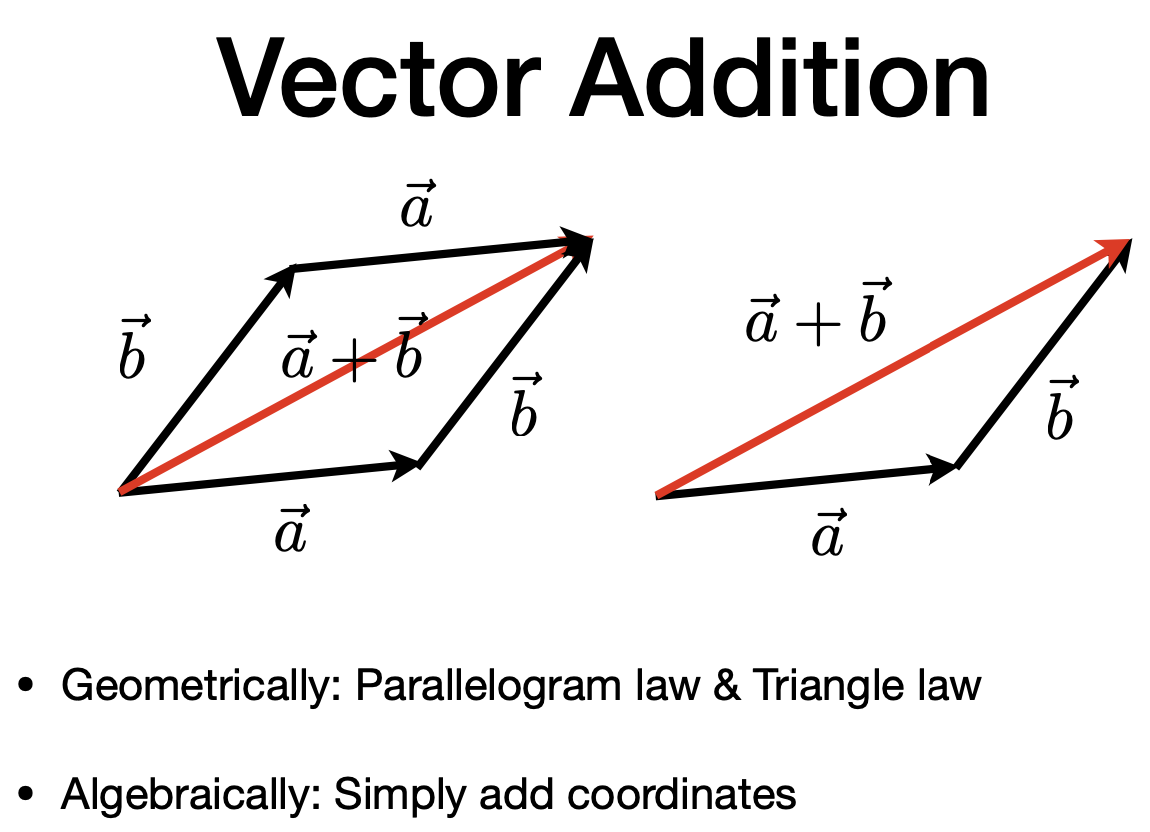
• Geometrically: Parallelogram law & Triangle law
• Algebraically: Simply add coordinates

Cartesian Coordinates

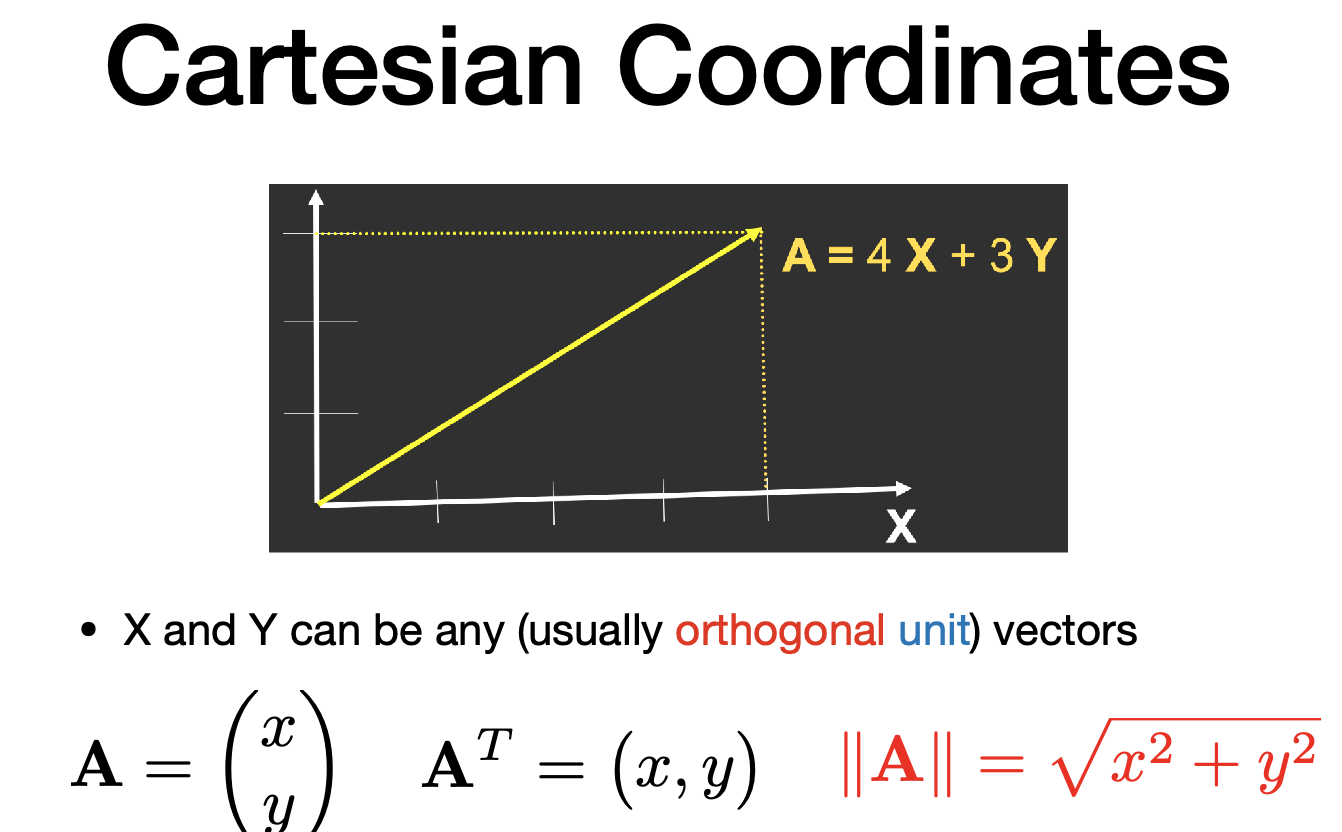
• X and Y can be any (usually orthogonal unit) vectors
  • $A =
    \left{
    \begin{matrix}
    x\
    y
    \end{matrix}
    \right}$
  • $A = | A^T = (x,y) |$
  • $||A|| = \sqrt{x^2 + y^2}$

Vector Multiplication

• Dot product
• Cross product
• Orthonormal bases and coordinate frames

Dos (scalar) Product 点乘

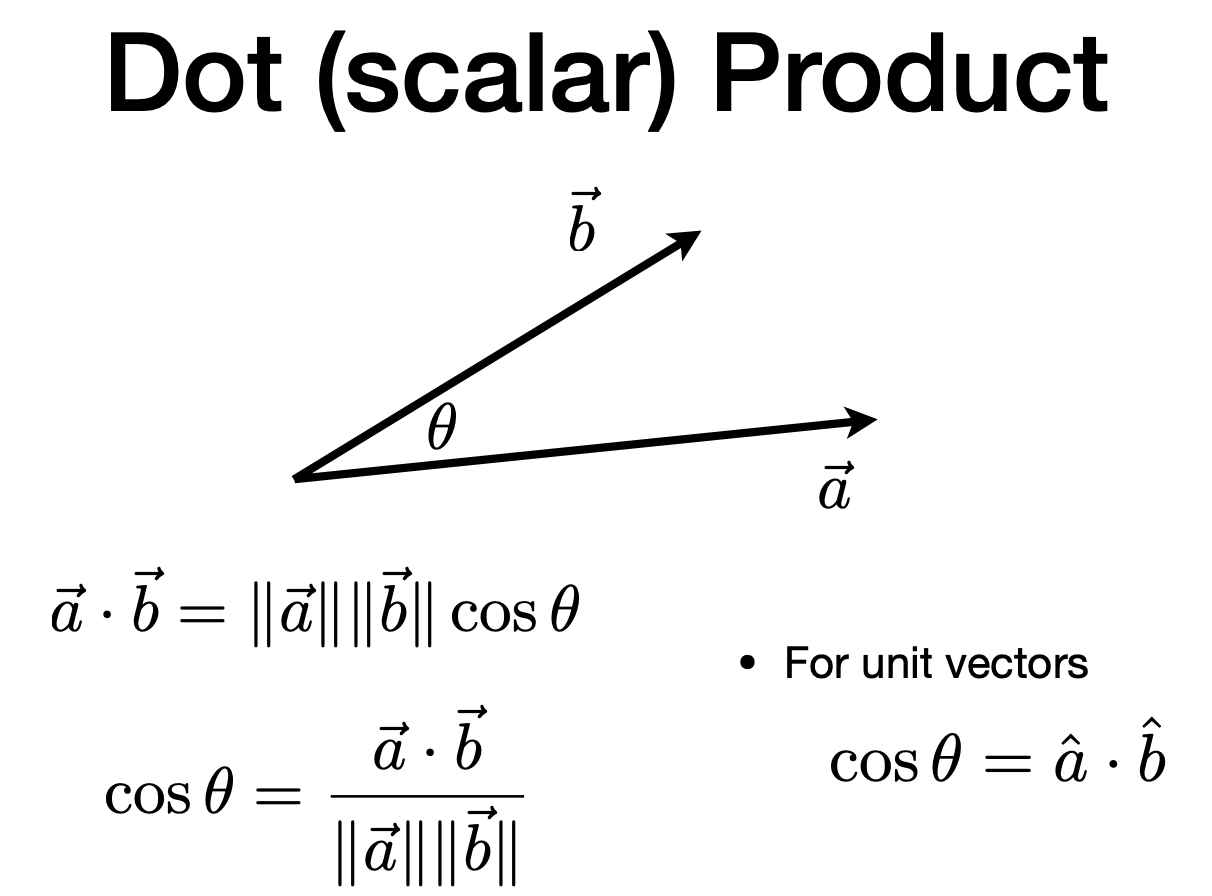
• Properties

  

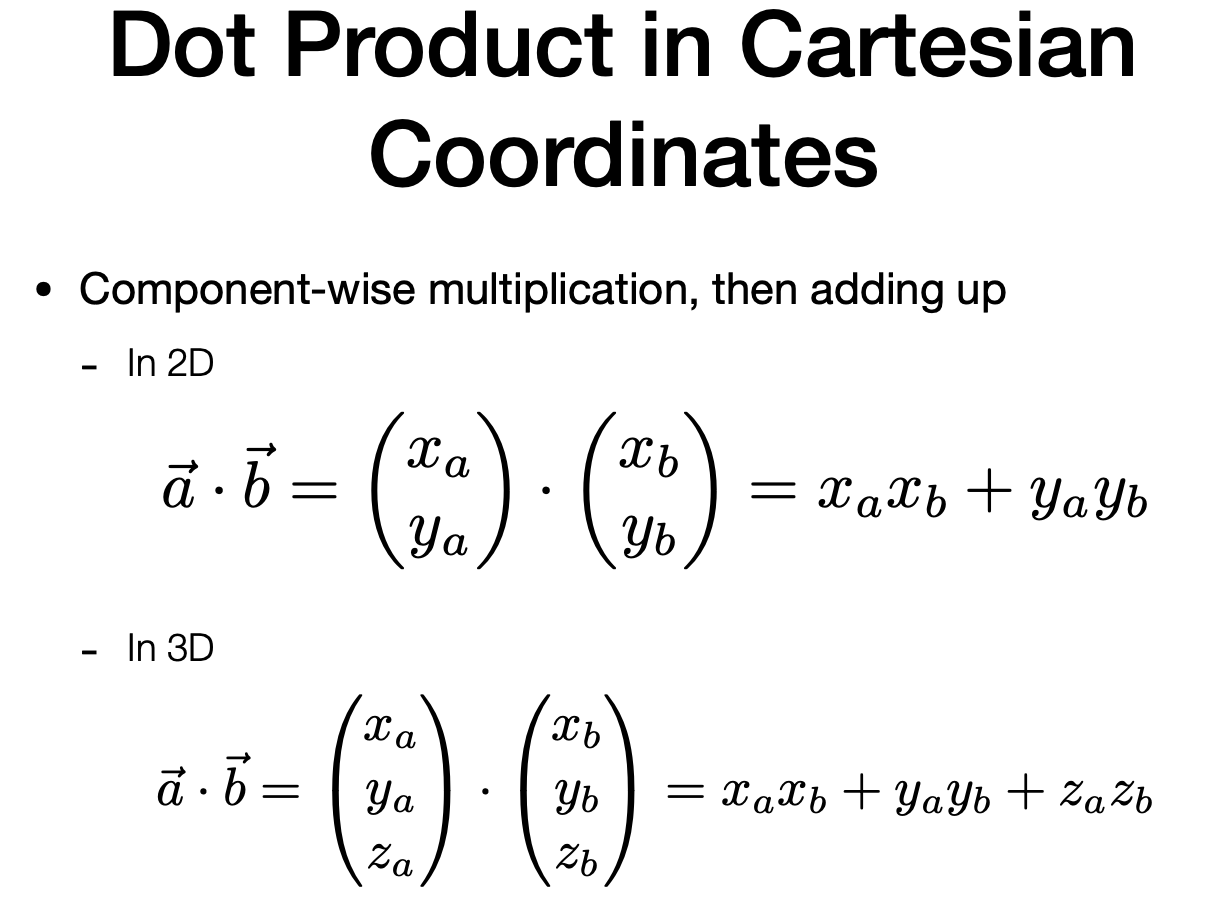
• Dot Product in Cartesian Coordinates

  

• Dot Product in Graphics

  • Find angle between two vectors
    (e.g. cosine of angle between light source and surface) 找夹角
  • Finding projection of one vector on another 找投影

• Dot Product for Projection

  

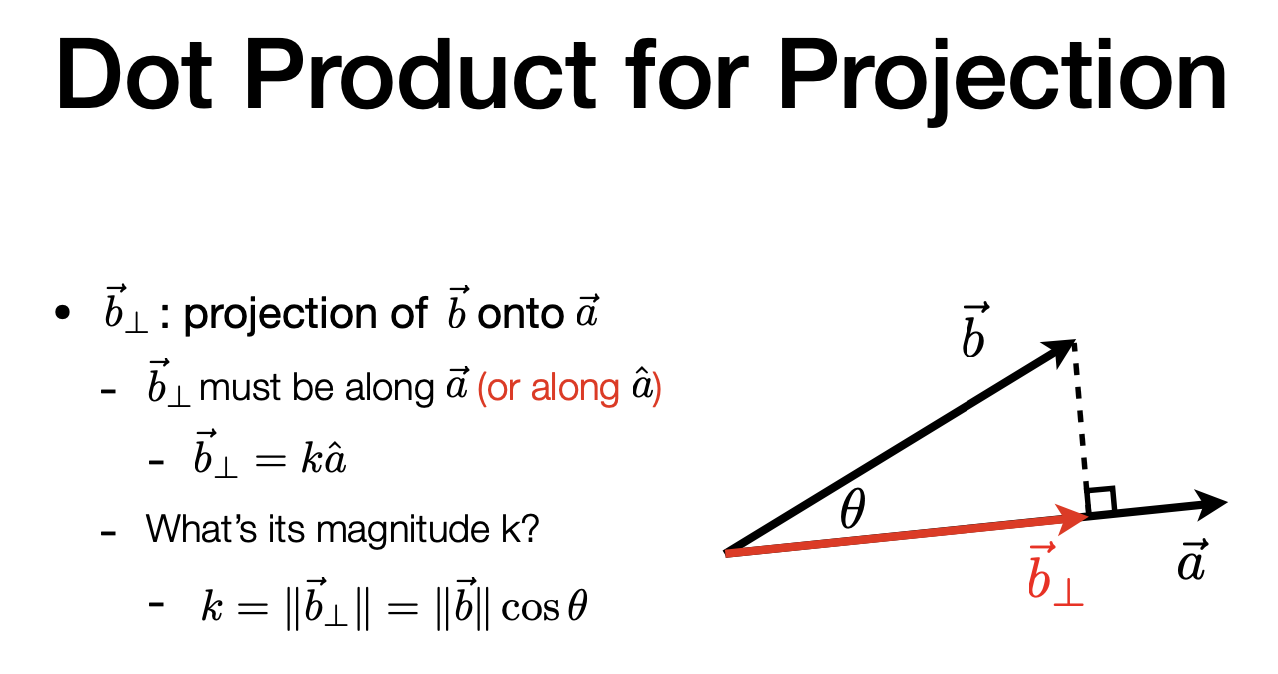
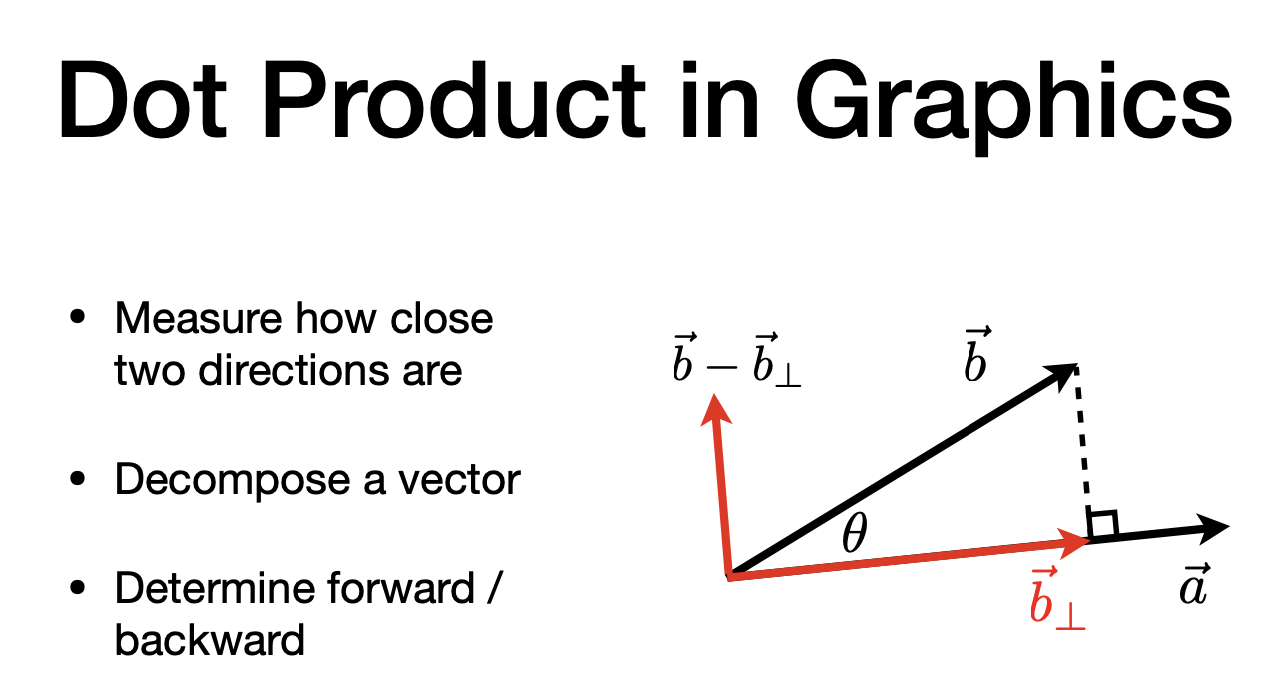
  • Measure how close two directions are （两个向量方向上接近就是1 垂直就0 相反就-1）

    

  • Decompose a vector

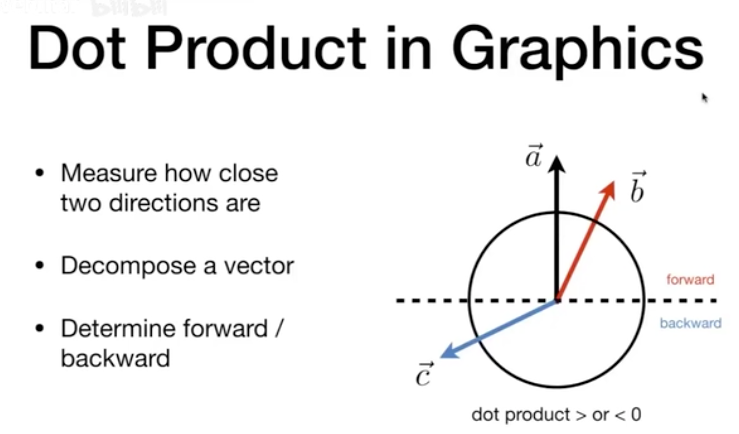
  • Determine forward / backward

    • 应用：镜面反射 入射光 高光

Cross product

• Cross (vector) Product

  
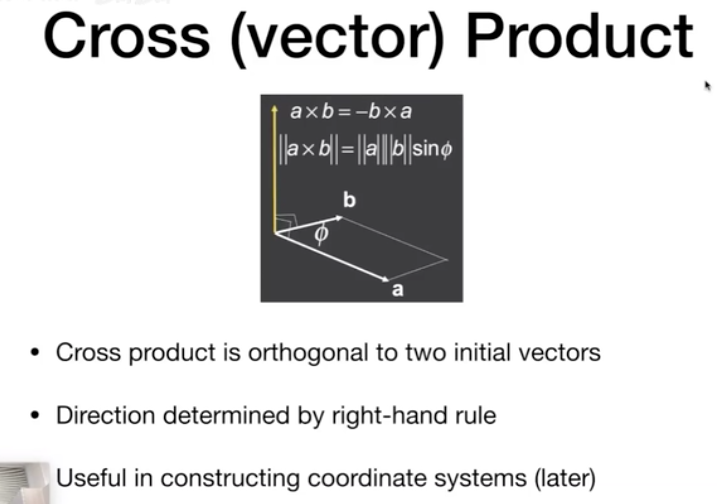
  • Cross product is orthogonal to two initial vectors
  • Direction determined by right-hand rule 不满足交换律
  • Useful in constructing coordinate systems (later)

• Properties

  
  • 向量叉乘得到的还是向量

• Cartesian Formula

  

• Cross Product in Graphics 应用

  • Determine left / right 左侧-叉乘结果为正

    

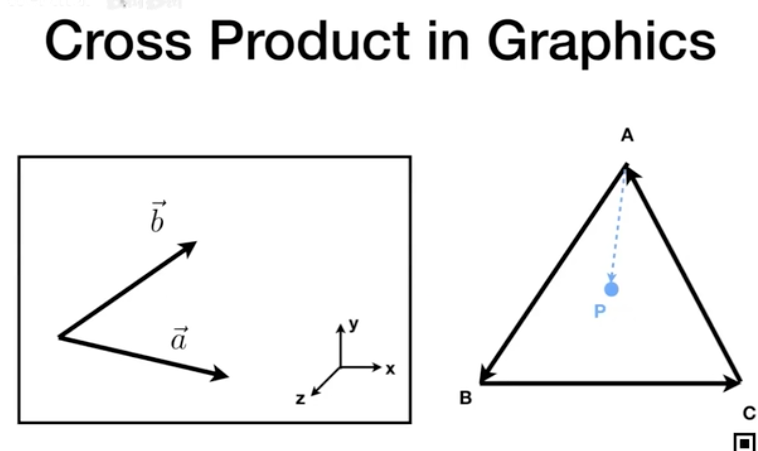
  • Determine inside / outside

    ab x ap
    bc x bp
    ca x cp
    如果三个结果符号相同 那么就在内部 若结果为0则为Cornercase 可内可外

  • 应用 - 光栅化

Orthonormal Bases / Coordinate Frames

• Important for representing points, positions, locations

• Often, many sets of coordinate systems

• Global, local, world, model, parts of model (head, hands, …)

• Critical issue is transforming between these systems/ bases

• A topic for next week

• Orthonormal Coordinate Frames 坐标系

  

---

Matrices

• Magical 2D arrays that haunt in every CS course

• In Graphics, pervasively used to represent transformations

  • Translation, rotation, shear, scale (more details in the next lecture)

• What is a matrix

  

• Matrix-Matrix Multiplication

  

• Properties

  • Non-commutative
    (AB and BA are different in general)

  • Associative and distributive

    • (AB)C=A(BC)
    • A(B+C) = AB+AC
    • (A+B)C = AC + BC

  • Matrix-Vector Multiplication

    • Treat vector as a column matrix (mx1)

    • Key for transforming points (next lecture)

    • Official spoiler: 2D reflection about y-axis

      

  • Transpose of a Matrix

    

  • Identity Matrix and Inverses

    

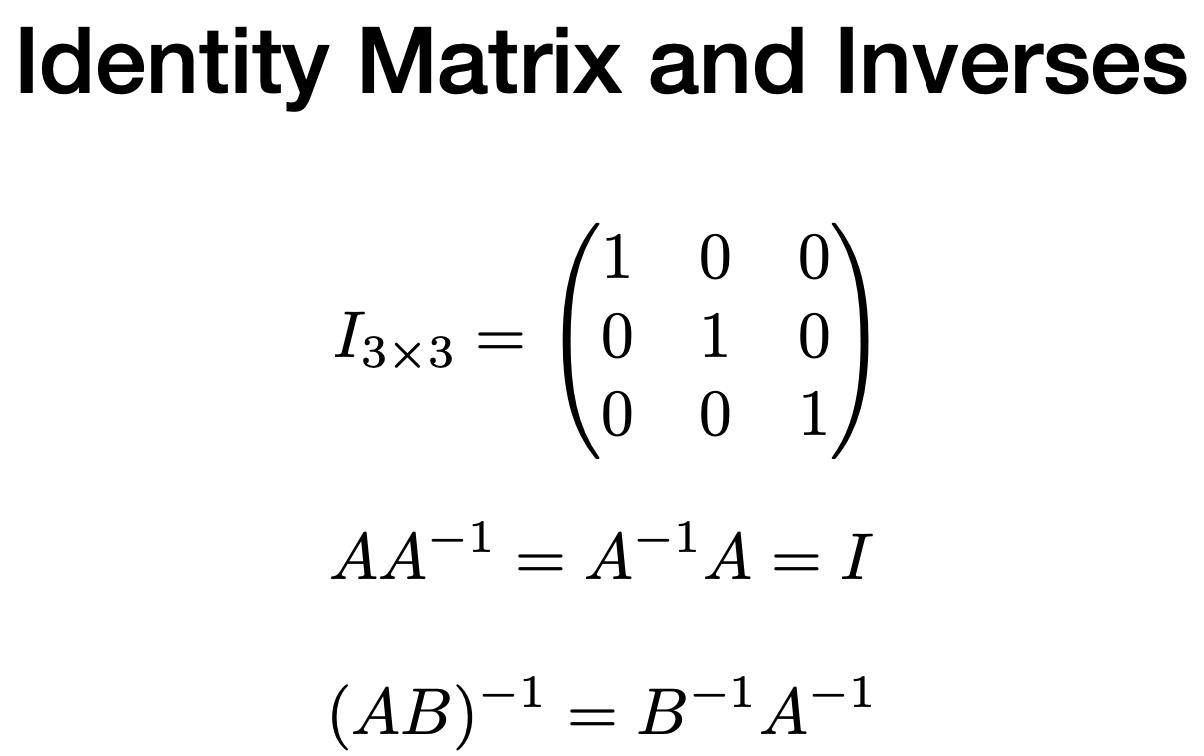
  • Vector multiplication in matrix form